Decidir se é verdadeira ou falsa cada uma das afirmações:

Se , e , então ou .

Vamos lá, vamos analisar os vetores:

Temos que os dois vetores são paralelos, assim eles estão na mesma direção, e o módulo do vetor é , ou seja, ele possui de comprimento, e o de é , possuindo de comprimento.

Entretanto não sabemos nada sobre o sentido a partir dos dados do enunciado, assim se temos que e possuem o mesmo sentido, vamos ver como fica isso na figura abaixo:

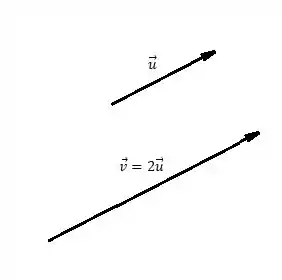
Mas também podemos ter , e aqui temos que e possuem sentido contrário, vamos ver isso na figura abaixo:

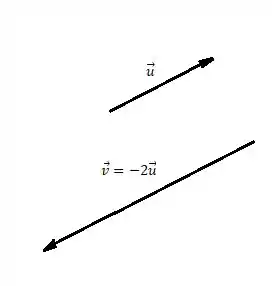
Assim aqui a afirmação é verdadeira!