Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 15
Demonstrar que o segmento de extremos nos pontos médios dos lados não paralelos de um trapézio é paralelo às bases e igual à sua semissoma.
Passo 1
Então pessoal, antes de tudo, a fim de facilitar nossa visualização sobre o problema, vamos esboçar aqui a figura de um trapézio e seus pontos médios, saca só:
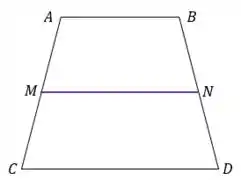
Vamos considerar esse trapézio de vértices , , e , no qual o segmento de reta é a ligação entre os pontos médios da figura.
Passo 2
Observando a figura, temos as seguintes informações, galera:
Além disso, temos:
Vale ressaltar aqui que os vetores que substituímos por de algum outro vetor, são porque eles equivalem à metade de um dos lados do trapézio, tudo bem? Se somarmos essas duas expressões de teremos:
Simplificando:
Passo 3
Se observarmos bem a figura do passo 1 com o resultado que acabamos de encontrar notaremos que e são paralelos e, portanto, o módulo da soma desses vetores é a soma dos seus módulos, se liga:
E disso nós tiramos que o módulo de é a semissoma das bases do trapézio, como queríamos demonstrar desde o início!
E está aí nossa resolução, pessoal! 😉
Resposta
Ei, a resposta está no passo a passo :)