Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 14

Demonstrar que os pontos médios dos lados de um quadrilátero qualquer são vértices de um paralelogramo.

Passo 1

Então galera, inicialmente vamos imaginar um quadrilátero qualquer, tudo bem? A fim de facilitar nossa visualização sobre o problema, vamos pegar um quadrilátero já conhecido, que é o trapézio. Vale ressaltar que a demonstração será válida com QUALQUER quadrilátero, beleza? Show! Desenhando o trapézio:

Os pontos A , B , C e D são pontos do nosso quadrilátero. Além disso, para complementar nosso desenho, vamos desenhar os pontos referentes aos pontos médios dos lados do nosso quadrilátero, saca só:

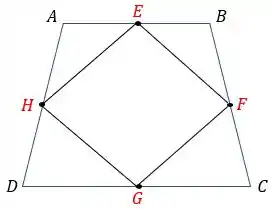
Como ilustrado, os pontos E , F , G e H são pontos médios dos seguimentos de reta A B - , B C - , C D - e D A - , nessa ordem.

Passo 2

Para provarmos que E F G H é, de fato, um paralelogramo, pelo que vimos em geometria devemos provar o seguinte:

E F → = H G →

Ou, em outras palavras:

F - E = G - H

Que é uma outra notação de vetores, tudo bem? Show! Da equação para o cálculo do ponto médio, temos o seguinte, pessoal:

Para E :

E = 1 2 A + B

Para F :

F = 1 2 B + C

Para G :

G = 1 2 ( C + D )

E, por fim, para H :

H = 1 2 D + A

Vamos guardar essas informações!

Passo 3

Vamos substituir na igualdade   F - E = G - H as informações que encontramos no passo anterior, se liga:

E F → = F - E

E F → = 1 2 B + C - 1 2 A + B

E F → = 1 2 B + 1 2 C - 1 2 A - 1 2 B

Simplificando:

E F → = 1 2 C - A

Agora aqui vem um bizu, pessoal! Somando e subtraindo o ponto D , teremos o seguinte:

E F → = 1 2 C + D - D - A

Note que não estamos alterando em nada o resultado, é apenas uma manipulação matemática, ok? Continuando:

E F → = 1 2 C + D - 1 2 D + A

De acordo com o que estabelecemos no passo 2:

E F → = G - H

∴ E F → = H G →

Que é exatamente o que queríamos demonstrar!

E está aí nossa resposta, galera! 😊

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine uma equação para a reta no plano que é paralela ao vetor V = ( 2,3 ) e passa pelo ponto P 0 = 1,2 .
Mostre que se os vetores u e v têm o mesmo comprimento então u + v e u – v são ortogonais. E a recíproca?
Seja P um ponto interior ao triangulo ABC tal que P A → + P B → + P C → = 0 . Prove que as retas AP, BP e CP são medianas de ABC, logo P é o baricentro desse triângulo.
Dado um triângulo acutângulo ABC no espaço, mostre que é sempre possível escolher os eixos de modo que as coordenadas dos vértices sejam A = (a, 0,0 ), B = (0,b,0) e C (0,0,c)
Seja P : a projeção ortogonal sobre a reta y = 3x. Dado o vetor u = (2, 5), determine x de tal modo que, pondo v = (x, 10), tenha-se Pv = Pu.