Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 37
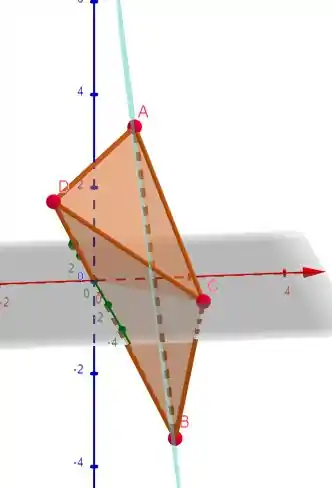
Descreva, em cada caso, a interseção entre o plano e o tetraedro de vértices , e
Passo 1
Substituindo os pontos no plano da letra nós teremos:
Como tem mudança de sinal então a reta atravessa o plano
Então o plano está no ponto e atravessa as arestas e . Simples assim.
Passo 2
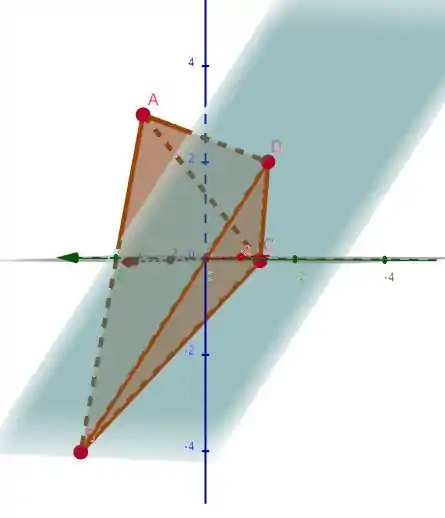
Agora aplicando os pontos no plano da letra :
Então pertence ao plano
Então como os outros pontos estão negativos (sem mudança de sinal entre um ponto e outro), logo o plano somente atravessa a pirâmide em
Passo 3
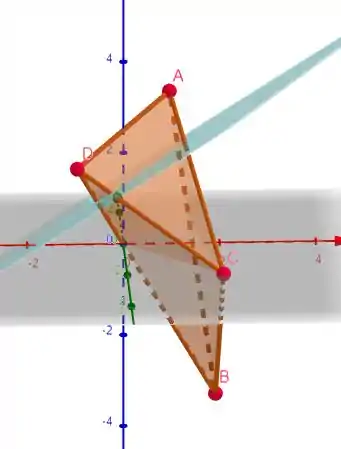
Agora aplicando os pontos no plano descrito em nós teremos:
Então esse plano atravessa as arestas e , justamente por inverter o sinal entre um ponto e outro.
Passo 4
Aplicando os pontos no plano descrito em d nós temos:
Então os pontos e (a reta AB também) pertencem ao plano e corta a aresta .
Passo 5
Finalmente aplicando os pontos no plano escrito em :
Então o plano é a face do tetraedro formado pelos pontos .
