Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 19.Exercício - Ex. 32
32- O vértice de uma pirâmide regular é e sua base é um quadrado de centro , contido em . Um dos lados do quadrado tem extremidades e e é uma diagonal. Obtenha uma equação geral do plano que contém a reta e forma ângulo de com o plano .
Passo 1
Pelos dados da questão o quadrado está no plano e esses quatro pontos valem:
Uma vez que os pontos e em ordem nos entregam um quadrado de lado 1 e o ponto que é o vértice deve estar no ponto médio dos pontos no plano . Sem contar que temos uma pirâmide regular.
Logo a reta será uma reta igual a:
Passo 2
As equações planares de serão iguais a:
Portando o feixe de planos que contém a reta serão iguais a:
E um vetor normal para esse plano será:
Passo 3
Agora vamos encontrar o vetor normal no plano formado pelos pontos , sabendo que ele tem uma equação geral de:
Aplicando os pontos teremos:
Diminuindo a primeira equação pela segunda nós encontraremos , logo:
e
Ou algo como:
Portanto um vetor normal para o plano será:
Passo 4
Como os dois vetores formam entre si um ângulo de então:
Elevando ao quadrado os dois lados nós teremos:
Então pode ser igual a , aplicando isso em , nós teremos:
Para
Para :
Já temos os dois planos :D
Plotando os pontos e os gráficos dos planos nós teremos:
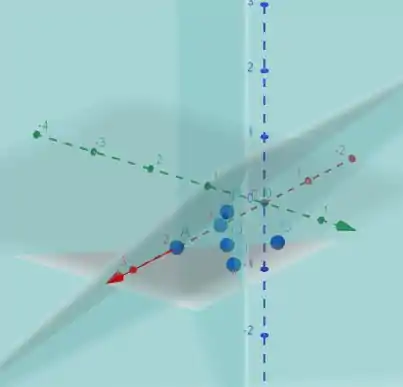
Esses planos passam pelas diagonais do quadrado.
Resposta
e