Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 2a

Determine as cônicas representadas pelas equações abaixo, encontrando também seus focos, diretrizes e excentricidade.

25 x 2 + 9 y 2 - 72 y - 81 = 0

Passo 1

Temos um termo linear de y na nossa equação, precisamos completar o quadrado e ficar com algo do tipo y 2 - 2 y o y + y o 2 que podemos reescrever como y - y o 2 e teremos uma cônica de origem 0 ,   y o . Vamos começar colocando 9 em evidência e ir fazendo uma álgebra pra chegar no que queremos.

25 x 2 + 9 ( y 2 - 8 y - 9 ) = 0

Daquele segundo termo dentro do parêntese, temos que:

8 = 2 y o

Daí temos que y o = 4 .

25 x 2 + 9 ( y 2 - 2 ∙ 4 y - 9 ) = 0

Passo 2

Precisamos ficar com 16 (que é y o 2 ) para completar o quadrado ao invés de - 9 como termo independente dentro do parêntese. Ou seja:

- 9 + x = 16

Temos que somar esse x , que é igual a 25 . Somando 9 ∙ 25 dos dois lados da equação vamos ficar com:

25 x 2 + 9 y 2 - 2 ∙ 4 y + 16 = 225

Agora sim! Podemos simplificar:

25 x 2 + 9 y - 4 2 = 225

Dividindo tudo por 225 :

x 2 9 + y - 4 2 25 = 1

Na forma canônica:

x 2 3 2 + y - 4 2 5 2 = 1

Agora sim! Temos uma elipse deslocada, com usa origem em 0 ,   4 e seu eixo maior no eixo y . Temos que a = 5 e b = 3

Passo 3

Temos o seguinte gráfico:

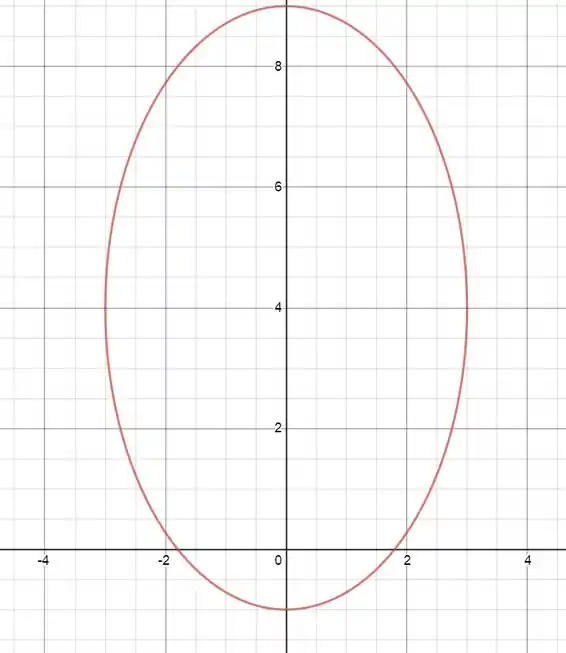
Passo 4

Seus focos são dados por F 1 = 0 ,   y o - c ; F 2 = ( 0 ,   y o + c ) .

c = 5 2 - 3 2 = 4 → F 1 = 0 ,   0 ; F 2 = 0 ,   8

Sua excentricidade é dada por:

e = c a = 4 5

Retas diretrizes dadas por:

y = - a e + y o ; y = a e + y o

→ y = ± 5 4 5 + 4

y 1 = - 9 4 ; y 2 = 41 4

Resposta

F 1 = 0 ,   0 ; F 2 = 0 ,   8

y 1 = - 9 4 ; y 2 = 41 4

e = 4 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 16 y 2 - 9 x 2 = 144
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. x 2 - 9 y 2 = 9
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 9 y 2 - 16 x 2 = 1
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. 9 x 2 - 18 y 2 + 54 x - 36 y + 79 = 0
Ache o centro, os vértices, os focos e as equações das assíntotas da hipérbole dada. Faça um esboço da curva e de suas assíntotas e mostre os focos. x 2 - y 2 + 6 x + 10 y - 4 = 0