Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 11.7.2 - Ex. 1h
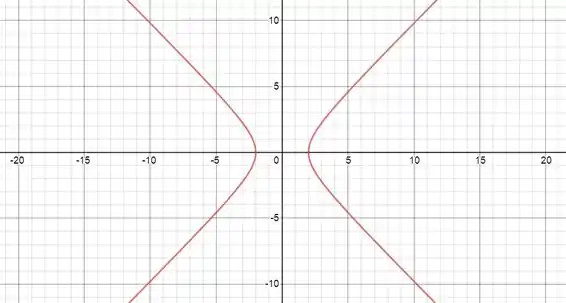
Esboce o gráfico das cônicas a seguir, determinando seus focos, diretrizes e excentricidade.
Passo 1
Temos um sinal negativo no ! Então temos uma hipérbole que não toca o eixo . Colocando na forma canônica:
Daí temos que
Passo 2
Esboçando essa hipérbole, ficamos com uma hipérbole bem quadradinha, já que .
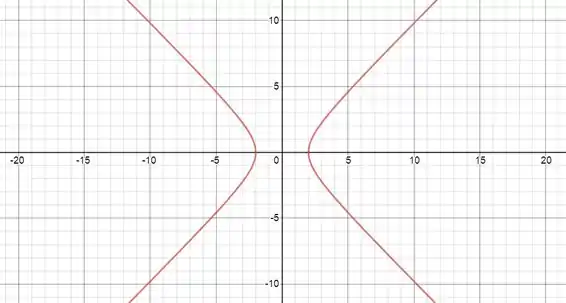
Passo 3
Para seus focos e temos que encontrar .
Então seus focos estarão em e .
Para a excentricidade da hipérbole, ficamos com:
E suas diretrizes serão as retas:
Resposta
Exercícios de Livros Relacionados
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Focos em - 1 ,4 e 7 ,4 e comprimento do eixo transverso 8 3 .
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Centro em - 2 ,- 1 , um vértice em - 2 ,11 e um foco - 2 ,14 .
Os vértices de uma hipérbole estão em - 3 ,- 1 e - 1 ,- 1 , e a distância entre os focos é 2 5 . Ache (a) a equação da hipérbole e (b) a equação das assíntotas.
Ache a equação da hipérbole satisfazendo as condições dadas e faça um esboço do gráfico.Um foco em - 3 - 3 13 ,1 , as assíntotas interceptam-se em - 3 ,1 e uma assíntota passa pelo ponto 1 ,7 .
Ache a equação da reta tangente à hipérbole 4 x 2 - y 2 = - 1 no ponto 1 2 ,2 .