Determine o menor valor que x + 2y assume no conjunto definido pelas desigualdades

Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??

Vamos começar analisando o sistema de desigualdades:

Neste caso, nossa região está delimitada acima de quatro retas dadas por:

Traçamos um gráfico dessas quatro retas, teremos que a nossa região é dada por:

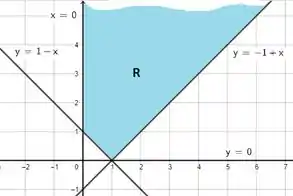
Um método prático de achar o valor mínimo para x+2y consiste em calcular esse valor para todo vértice P da nossa região R e ver qual desses valores é o menor.

Observando mais atentamente o gráfico da nossa região, encontramos os vértices A=(1,0) e B(0,1).

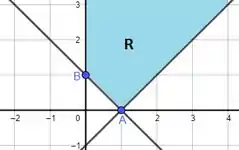
Calculando o valor da expressão x + 2y para cada um dos pontos, temos:

Para A, x + 2y = 1 + 2.0 = 1;

Para B, x + 2y = 0 + 2.1 = 2.

Logo, o ponto A determina o menor valor para x + 2y.