Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 4.Exercícios Propostos - Ex. 23
Determine , e para que seja uma base ortonormal positiva.
Passo 1
Ok, galera, vamos começar relembrando a definição de base positiva: base positiva é aquela na qual os produtos vetoriais entre dois vetores da base devem ter como resultado o terceiro vetor, com sinal positivo. Acredite se quiser, é só isso mesmo! Então, vamos calcular os produtos vetorial dos vetores , com .
O produto interno do primeiro vetor de base com o segundo deve resultar no terceiro com sinal positivo:
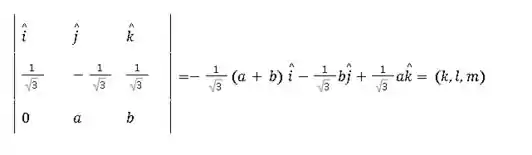
Vamos multiplicar a primeira equação por (a razão para isso vai ficar clara daqui a pouco):
Ok, vamos deixar esse resultado reservado por enquanto. O produto vetorial do segundo e terceiro vetores deve resultar no primeiro com sinal positivo:
Esse produto vetorial gerou as condições:
Vamos somar a segunda e a terceira equações:
Agora, lembra aquele resultado que nós deixamos reservado? Vamos comparar com o resultado acima
Agora que sabemos o valor de , com exceção de um sinal que ainda deve ser determinado, podemos obter e :
Agora podemos obter e :
Passo 2
Tá, mas ainda temos que determinar o sinal de todos as incógnitas. Vamos calcular o último produto vetorial, que é do terceiro vetor com o primeiro, resultado no segundo:
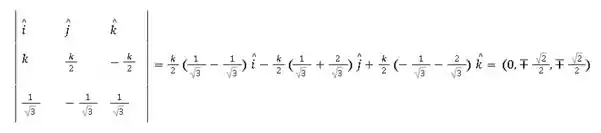
Que basicamente resulta em . Vamos retornar a primeira condição obtida pelo determinante da base:
É…, essa opção não é muito conclusiva. Bom, pelo menos vimos que a base será positiva independentemente do sinal de , então podemos escolher . Assim, ficamos com