Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 24b
24. Calcular a área do triângulo e a altura relativa do lado , dado que:
a) e ;
b) e
Passo 1
(b) Bem... Como nós temos três pontos... Veja na figurinha que é meramente ilustrativa.
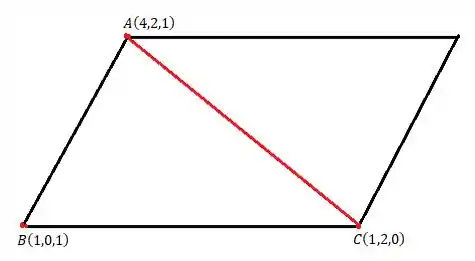
Desenhamos um paralelogramo, pois “a área do paralelogramo formado determinado pelos vetores e é NUMERICAMENTE igual ao comprimento do vetor ”.
Então, fazendo o módulo de , encontramos a área do paralelogramo.
Repare, também, na linha vermelha que eu fiz... Então a área do triângulo vai ser:
E lembrando aqui rapidinho que o produto vetorial de dois vetores e .
Passo 2
Vamos começar, então, calculando cada vetor:
Passo 3
Agora vamos fazer o produto vetorial:
Resolvendo o determinante:
Calculando o módulo:
Então a área do triângulo:
Passo 4
Agora vamos calcular a altura relativa ao lado .. Lembra que a área de um triângulo é:
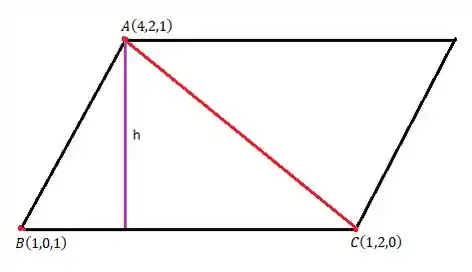
A área a gente já calculou no passo anterior, a altura é o que a gente quer achar e a base é o lado , né...
Então podemos calcular o módulo de ...
Então podemos achar a altura: