é uma base ortonormal positiva.
- Determine , sabendo que ele é paralelo ao vetor .
- Determine , sabendo que é da forma .
- Determine a que .
Passo 1
Galera, vamos resolver os três itens ao mesmo tempo. Como é paralelo ao vetor , então . Também já vamos usar a informação do item b), que é da forma . O vetor será da forma . Assim, temos seis incógnitas para determinar: .
Passo 2
Vamos continuar agora calculando os produtos vetoriais:
- Do primeiro vetor com o segundo:
- Do segundo vetor com o terceiro:
- Do terceiro vetor com o primeiro:
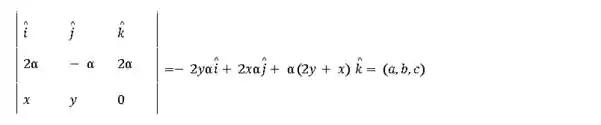
Então,
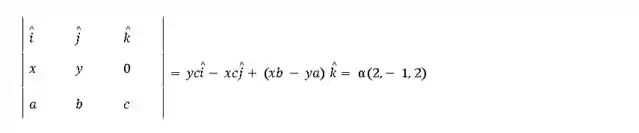
Temos
onde substituímos . Igualando a primeira e a terceira equações, obtemos
Por enquanto, temos
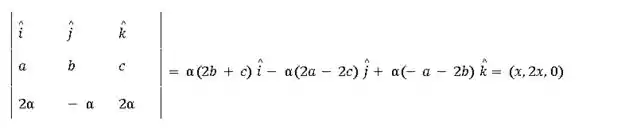
Substituindo na primeira equação, obtemos
Além disso,
Então, escrevemos quase tudo em termos de , exceto:
Vamos substituir os resultados acima em:
Logo,
; ;
Passo 3
Agora, só precisamos substituir ; e nas demais incógnitas: