Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 2ª Edição - Alfredo Steinbruch e Paulo Winterle- Ed: 2º - Capítulo 7.5 - Ex. 21
Efetuar uma rotação nos eixos coorenados a fim de eliminar o termo em . Identificar a cônica e escrever sua equação no sistema obtido após a rotação. Esboçar o gráfico.
Passo 1
Pra resolver essa questão, vamos usar de novo o método dos invariantes. Como só vimos uma questão com isso até agora, ainda tá muito fresco na cabeça, e por isso vou repetir o método todo. É assim: a equação completa da cônica é:
Quando a gente fizer a rotação da cônica, o termo em vai sumir. A gente chama de invariantes porque tem algumas expressões que não mudam o valor, nem quando a gente roda a cônica. São eles:
Essas letras, , , e serão os coeficientes da equação da cônica, já desrotacionada. Repara no seguinte: , já que estamos com a cônica desrotacionada. Tem que saber também que esse da segunda equação é o ângulo de rotação da cônica, que a gente calcula como:
Se por acaso , a tangente vai tender ao infinito. Isso quer dizer que , e aí o ângulo de rotação . Beleza, já relembramos tudo, agora vamos resolver essa parada.
Passo 2
A equação da nossa cônica é:
Comparando com a equação completa da cônica, a gente tem:
Vamos encontrar o ângulo de rotação:
O que a gente precisa aqui é do seno do ângulo, então bora mexer nessa expressão pra descobrir:
Substituindo na relação fundamental:
Passo 3
Show, já temos tudo que precisávamos! Vamos ver os invariantes.
Resolvendo o sistema das duas primeiras linhas, vamos encontrar e . Beleza, então já sabemos a equação da cônica no sistema !
Dividindo tudo por e passando o termo independente pro outro lado:
Essa equação representa uma elipse!
Passo 4
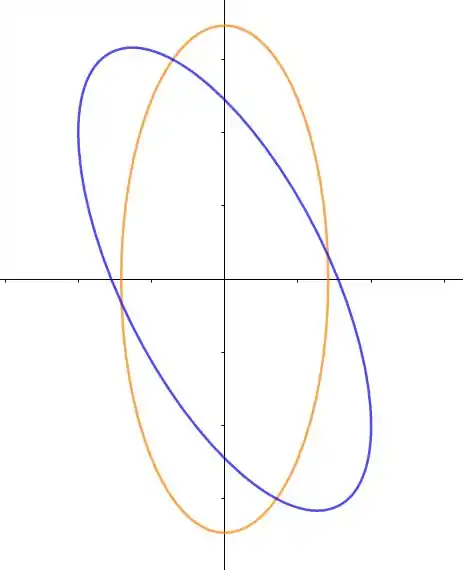
Fazendo o esboço delas:
