Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 48a
Encontrar o vértice oposto a , no paralelogramo , para
, e
Passo 1
Primeiro vamos ter uma noção dos pontos no paralelogramo:
Temos então que o vértice oposto à é o ponto , e para encontrar ele podemos analisar os vetores e :
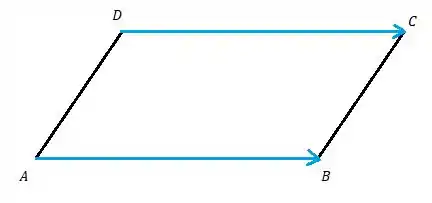
Dá pra perceber que os vetores são iguais, assim temos a expressão:
Passo 2
Vamos então resolver a igualdade dos vetores e para achar o ponto :
Pronto, temos que o vértice oposto a é .
Resposta
Exercícios de Livros Relacionados
Determine uma equação da esfera com centro em ( 0 , 1 , - 1 ) e raio 4 . Qual é a intersecção dessa esfera com o plano y z ?
Determine se os pontos estão em uma mesma reta. A 2 , 4 , 2 ,B 3,7 , - 2 ,C ( 1,3 , 3 ) D 0 , - 5,5 ,E 1 , - 2,4 ,F ( 3,4 , 2 )
Encontre os comprimentos dos lados do triângulo P Q R . Ele é um triângulo retângulo? É isósceles?8. P 2 , - 1,0 ,Q 4,1 , 1 ,R ( 4 , - 5,4 )
Encontre os comprimentos dos lados do triângulo P Q R . Ele é um triângulo retângulo? É isósceles?7. P 3 , - 2 , - 3 ,Q 7,0 , 1 ,R ( 1,2 , 1 )
Determine uma equação da esfera com centro em ( 2 , - 6 , 4 ) e raio 5 . Descreva sua intersecção com cada um dos planos coordenados.