Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.9 - Ex. 9

Encontre a matriz canônica do operador T   :   R 3   →   R 3 definido por

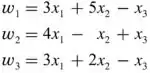
e depois calcule T ( - 1 ,   2 ,   4 ) por substituição direta nas equações e também por multiplicação matricial.

Passo 1

Olá!! Tudo bem? Primeiro devemos encontrar a matriz canônica, então temos:

T = 3       5 - 1 4 - 1       1 3       2 - 1

Então, para x , y , z = ( - 1 ,   2 ,   4 ) , temos:

w 1 = 3 - 1 + 5 2 + - 1 ( 4 ) = 3

w 2 = 4 - 1 + - 1 2 + 1 4 = - 2

w 3 = 3 - 1 + 2 2 + - 1 4 = - 3

O que significa T - 1 ,   2 ,   4 = ( 3 , - 2 , - 3 ) .

Por multiplicação matricial temos:

3       5 - 1 4 - 1       1 3       2 - 1 - 1       2       4 =       3 - 2 - 3

Resposta

Veja a resolução.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a multiplicação matricial para encontrar a reflexão de 2 ,- 5 ,3 no plano x z .
Use a multiplicação matricial para encontrar a imagem do vetor ( 3 ,- 4 ) se for girado por um ângulo de θ = 45 ° .
Use a multiplicação matricial para encontrar a imagem do vetor ( 3 ,- 4 ) se for girado por um ângulo de θ = - 60 ° .
Use a multiplicação matricial para encontrar a reflexão de 2 ,- 5 ,3 no plano x y .
Use a multiplicação matricial para encontrar a reflexão de 2 ,- 5 ,3 no plano y z .