Enunciado
Álgebra Linear e Geometria Analítica - Um curso de geometria analítica e álgebra linear, Reginaldo J. Santos- Ed: 1º - Capítulo 5.4 - Ex. 2a
Encontre o ponto , se as coordenadas de em relação ao sistema de coordenadas , , são:
a) , em que
Passo 1
Eaew, tudo em cima contigo hoje?
Para resolver essa questão é bom dar uma relembrada em como fazemos uma mudança de coordenadas pela notação matricial, nós temos que:
Ou seja, o ponto no sistema de coordenadas , relacionado ao ponto na base canônica e uma matriz que é construída em termos do vetor de base do novo sistema de coordenadas, vamos usar os dados do enunciado nesta expressão, beleza?
Passo 2
Nós temos então que
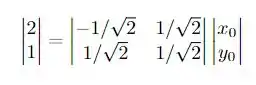
Fazendo o produto matricial temos que
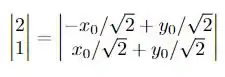
Isso nos dá um sistema de equações lineares que podemos resolver, bora fazer isso!
Passo 3
O sistema é tal que temos a equação:
e
Da equação (1) temos que
e, portanto, a equação (2) nos dá:
Usando este resultado em (3), temos:
Portanto, temos o ponto . A alternativa foi isso, vamos para a próxima!