Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Hipérbole - Ex. 13b
13. Esboçar o gráfico de uma hipérbole (com suas assíntotas) de centro , eixo real sobre e excentricidade:
b)
Passo 1
Então pessoal, a equação de uma hipérbole com centro em e eixo real sobre possui o seguinte formato, conforme estudamos:
Show! A única informação que temos é referente à excentricidade da hipérbole dada, certo? Então devemos explorar ao máximo essa informação. Para esse formato de hipérbole, a excentricidade da mesma é dada pela seguinte razão:
Como nos foi dito que , então por comparação:
Beleza, encontramos e , agora falta encontrarmos !
Passo 2
Para encontrarmos basta utilizarmos o Teorema de Pitágoras, galera! Se liga:
Substituindo os valores que encontramos:
Agora que temos e , podemos escrever a expressão da nossa hipérbole, que é:
E o gráfico seria:
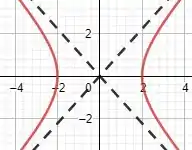
No qual as curvas em vermelho é a hipérbole e as linhas tracejadas em preto são as assíntotas. E está aí nossa resolução!
Resposta
