Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 6.Exercícios Propostos - Ex. 27
Escreva equações paramétricas da reta , perpendicular às retas e e que passa pela intersecção das mesmas. Dados:
e
Passo 1
Como vai, gente? Vamos começar essa questão escrevendo as equações paramétricas da reta :
Essa reta tem vetor diretor dado por . Como a reta é perpendicular às retas e , então o vetor diretor de é perpendicular aos vetores diretores de e . Os vetores diretores das retas e são, respectivamente
Passo 2
A questão nos diz que as retas e se interceptam num ponto. Qualquer ponto em e pode ser escrito como ou . Os dois pontos devem ser iguais na interseção, o que significa que
As duas equações tem o mesmo resultado: , enquanto a terceira resulta em . Essas duas equações só podem ser simultaneamente verdadeiras se e . Assim, ficamos com
Então, conseguimos mostrar que para e .
Passo 3
A reta que queremos deve passar pela interseção de e , ou seja, no ponto e tem vetor diretor . Nesse caso, ficamos com
Como a reta deve ser perpendicular a e , então seu vetor diretor deve ser paralela ao vetor obtido a partir do produto vetorial de e (que determinamos no Passo 1):
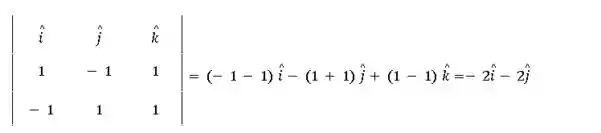
Ou seja, devemos ter
Como não temos nenhuma restrição para , podemos escolher um valor mais conveniente. Nesse caso, vamos escolher . Assim, ficamos com
e a equação paramétrica da reta se torna