Enunciado
Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 1.1 - Ex. 3e
Escrevendo em termos das suas colunas, , em que e , o produto pode ser escrito como (o caso deral está no Exercício 1.1 17 (a) na página 23).
Passo 1
Bem pessoal, esse exercício é bem parecido com os anteriores. Primeiro vamos fazer a multiplicação de A com B;
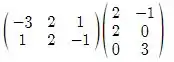
AB =
Fazendo a multiplicação vamos ter:
AB =
Fazendo a simplificação dos elementos vamos ter:
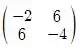
AB =
Passo 2
Agora vamos analisar a afirmação do enunciado, ele nos fala que AB = A [] = []
Sendo que e são as colunas de B:
Vamos verificar então:
=
=
Conseguimos concluir então que está correto.
Resposta
Conseguimos concluir que a afirmativa do enunciado está correto.
Exercícios de Livros Relacionados
Seja A uma matriz diagonal, isto é, os elementos que estão fora da diagonal são iguais a zero ( a i j = 0 para i ≠ j ) . Se a i i ≠ 0 , para i = 1 , … , n , mostre que A é invertível e a sua inversa e
Se A B = B A e p é um número inteiro positivo, mostre que A B p = A p B p .
Para matrizes quadradas A = a i j n x n definimos o traço de A como sendo a soma dos elementos da diagonal(principal) de A , ou seja, t r A = ∑ i = 1 n a i i .(b) Mostre que t r α A = α t r A
Já vimos que o produto de matrizes não é comutativo. Entretanto, certos conjuntos de matrizes são comutativo. Mostre que: (b)Se A é uma matriz nxn e B = a 0 I n + a 1 A + a 2 A 2 + … + a k A k em que
Sejam E 1 = 1 0 0 ⋮ 0 , E 2 = 0 1 0 ⋮ 0 , … , E n = 0 0 0 ⋮ 1 matrizes nx1 . (a) Mostre que se A = a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a m 1 a m 2 … a m n é uma matriz mxn , então A E j é igua