Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.5 - Ex. 12
Nos Exercícios 11-12, encontre a área do paralelogramo com os vértices dados.
12.
Passo 1
Para calcularmos a área de um paralelogramo, sabemos , porém como estamos tratando de vetores bidimensionais, podemos calcular a área desse paralelogramo, obtendo o valor absoluto do determinante da matriz composta por dois vetores, esses vetores vão ser correspondentes a base e a altura do paralelogramo, veja só:
Temos um paralelogramo formado pelos vértices e vetores indicados na figura:
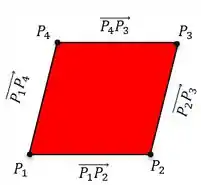
A partir da figura podemos retirar as seguintes informações:
Logo podemos escolher quaisquer dois vetores correspondentes a base e altura para calcularmos a área em vermelho desse paralelogramo.
Passo 2
Temos os seguintes os vértices: a partir deles vamos encontrar o vetores: e .
Passo 3
Agora temos os vetores: e , podemos encontrar a área:
Logo como queremos o valor absoluto do determinante, temos que .