Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 3.1 - Ex. 4c
Nos exercícios 3-4, em cada parte esboce o vetor dado com o ponto na origem.
- (c) (0,-7)
Passo 1
Esse vetor possui apenas duas coordenadas, então precisamos desenha-lo no . Juntando as duas coordenadas dadas:
O esboço deve ficar parecido com isso:
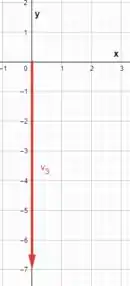
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Prove as partes e - ( h ) do Teorema 3.1 . 1 .
Prove: se S for uma base de um espaço vetorial V , então valem as relações seguintes com quaisquer vetores u e v e qualquer escalar k . u + v S = u S + v S
Prove: se S for uma base de um espaço vetorial V , então valem as relações seguintes com quaisquer vetores u e v e qualquer escalar k . (b) k × v S = k × v S
Se A e B não forem ambos nulos, então a equação A x+B y=0 representa uma reta pela origem em R 2 . O que representa essa equação em R 3 , se pensarmos nela como sendo A x+B y+0 z=0 ? Explique.
(a)Que tipo de objeto geométrico é o conjunto de todos osvetores em R 2 ortogonais a um vetor não nulo?(b)Que tipo de objeto geométrico é o conjunto de todos osvetores em R 3 ortogonais a um vetor não