Exercícios de Espaços Vetoriais - Lista de Exercícios Resolvida
Questão 1
Sobre os conjuntos:
E sabendo que é munido das operações:
- Se , então
- é um espaço vetorial
É correto afirmar sobre as afirmações acima que:
I e II são verdadeiras
I é verdadeira e II é falsa
I e II são falsas
I é falsa e II é verdadeira
Ver solução completaQuestão 2
Dado o espaço vetorial , foram definidas operações de soma e multiplicação por escalar, respectivamente:
Dentre as opções abaixo, marque a alternativa verdadeira:
O elemento neutro da soma é o vetor
O espaço vetorial não possui inverso aditivo
O elemento neutro da soma é
O elemento neutro da multiplicação é , pois
Ver solução completaQuestão 3
O elemento neutro para soma do espaço vetorial das funções reais é o(a):
Número zero
Função identidade
Função identicamente nula
Conjunto vazio
Ver solução completaQuestão 4
Considere o espaço vetorial munido do produto interno definido por:
Se são tais que é o elemento de mais próximo de , então é igual a:
Ver solução completa
Questão 5
Seja um espaço vetorial real de dimensão munido de um produto interno e seja uma base ortonormal de . Considere o subespaço vetorial de dado por
e seja . Temos que a projeção ortogonal de em é igual a:
Questão 6
Seja
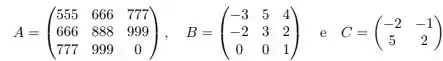
Assinale a alternativa correta:
(a) nem e nem são diagonalizáveis sobre os complexos e é diagonalizável sobre os complexos, mas não sobre ;
(b) é diagonalizável sobre e são diagonalizáveis sobre os complexos , mas
nem e nem são diagonalizáveis sobre ;
(c) são diagonalizáveis sobre R;
(d) são diagonalizáveis sobre e é diagonalizável sobre os complexos, mas não sobre ;
(e) são diagonalizáveis sobre os complexos, mas nenhuma delas é diagonalizável sobre .
Ver solução completaQuestão 7
Seja um espaço vetorial real de dimensão munido de um produto interno e sejam bases ortonormais de . Considere as seguintes afirmações:
(I) não é uma linha da matriz;
(II) as matrizes e possuem o mesmo determinante;
(III) se for um operador linear tal que a matriz seja simétrica, então a matriz também será simétrica.
Assinale a alternativa correta:
(a) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
(b) apenas as afirmações (I) e (III) são necessariamente verdadeiras;
(c) apenas as afirmações (I) e (II) são necessariamente verdadeiras;
(d) todas afirmações são necessariamente verdadeiras;
(e) apenas a afirmação (II) é necessariamente verdadeira.
Ver solução completaQuestão 8
Seja uma matriz real. Suponha que sejam raízes do polinômio característico de e que
em que denota o operador linear que é representado por na base canónica de . Assinale a alternativa correspondente a uma base do espaço das soluções reais do sistema de equações diferenciais
Questão 9
Seja o espaço vetorial de todas as funções deriváveis tais que a derivada seja contínua e . Considere munido do produto interno definido por
Para quaisquer Seja o subespaço vetorial de gerado por
Assinale a alternativa correspondente a uma base ortonormal de .
Questão 10
Considere o espaço vetorial munido do seu produto interno usual e os vetores:
, , e .
Aplicando-se o processo de ortogonalização de Gram–Schmidt ao conjunto , obtemos o conjunto ortogonal . Temos que a soma das coordenadas do vetor é igual a:
Questão 11
Seja um espaço vetorial munido de um produto interno e seja um
subconjunto linearmente independente de com elementos tal que
para todo . Assinale a alternativa correta:
(a) é uma base ortonormal de .
(b) é uma base ortogonal de , mas pode não ser uma base ortonormal de .
(c) pode não gerar .
(d) pode ter dimensão infinita.
(e) O conjunto pode não ser ortogonal.
Ver solução completaQuestão 12
Considere o espaço vetorial munido de seu produto interno usual e sejam:
Se são tais que é igual à projeção ortogonal de sobre o
o subespaço , então é igual a:
Questão 13
Considere o subespaço
do espa ̧co vetorial . Suponha munido de seu produto interno usual e sejam tais que
Temos que é igual a:
Questão 14
Considere o conjunto de matrizes da forma , com as seguintes operações de soma e multiplicação por escalar:
e
Assinale a alternativa FALSA:
A soma de dois elementos de está em .
vale para todo .
Todo elemento de possui inverso aditivo (negativo).
é um espaço vetorial.
Ver solução completaQuestão 15
Indique se cada afirmação abaixo é verdadeira ou falsa. Justifique.
(a) com as operações de soma e multiplicação por escalar abaixo não é espaço vetorial.
Ver solução completaQuestão 16
Seja o conjunto dos pares ordenados de números reais munido da soma usual. Considere as seguintes operações de produto por um escalar :
Quais das opções abaixo é verdadeira?
não é um espaço vetorial.
não é um espaço vetorial.
o produto é distributivo com relação à soma de escalares.
o produto não é distributivo com relação à soma vetorial.
Ver solução completaQuestão 17
Assinale a alternativa em que não é um subespaço do espaço vetorial :
Escolha uma opção:
- ;
- é o espaço das funções contínuas de em e é o conjunto das funções tais que ;
- é o espaço das funções deriváveis de em e é o conjunto das funções tais que , para ;
- e ;
- é o espaço de todas as funções de em e é o conjunto das funções tais que , para todo .
Questão 18
Considere as seguintes afirmações:
(I) se V for um espaço vetorial real de dimensão finita munido de um produto interno e e forem subespaços vetoriais de tais que , então a desigualdade
será válida para qualquer , em que denota a norma correspondente ao produto interno
(II) se for um inteiro positivo e for uma matriz diagonalizável, então o conjunto das soluções reais do sistema de equações diferenciais
será um subespaço vetorial de dimensão do espaço vetorial de todas as funções
(III) se denotar a base canônica de e se forem as coordenadas na base de um elemento do conjunto
então valerá que
(a) apenas as afirmações(I) e (II) são verdadeiras;
(b) apenas as afirmações (I) e (III) são verdadeiras;
(c) todas as afirmações são verdadeiras;
(d) apenas as afirmações (II) e (III) são verdadeiras;
(e) todas as afirmações são falsas.
Ver solução completaQuestão 19
Considere as seguintes afirmações:
(I) se for um espaço vetorial real de dimensão finita munido de um produto interno, for um operador linear e existir uma base ortonormal de tal que a matriz seja diagonal, então o
operador será simétrico;
(II) para qualquer inteiro positivo n e qualquer matriz , se as colunas de formarem uma base ortonormal de com respeito ao produto interno usual, então será igual à matriz identidade, em que denota a transposta da matriz ;
(III) se for um espaço vetorial real de dimensão finita munido de um produto interno e se forem bases ortonormais de , então a matriz será simétrica.
Assinale a alternativa correta:
(a) apenas as afirmações (I) e (II) são verdadeiras;
(b) todas as afirmações são verdadeiras;
(c) apenas as afirmações (II) e (III) são verdadeiras;
(d) apenas a afirmação (III) é verdadeira;
(e) apenas as afirmações (I) e (III) são verdadeiras.
Ver solução completaQuestão 21
Q3. Considere o espaço vetorial munido do seu produto interno usual e as bases
e
De . Se e são os operadores lineares tais que
e ,
Então:
a) é simétrico e não é simétrico;
b) e são ambos simétricos e têm polinômios característicos diferentes;
c) não é simétrico e é simétrico;
d) e são ambos simétricos e têm o mesmo polinômio característico;
e) nem nem são simétricos.
Ver solução completaQuestão 22
Q9. Considere o espaço vetorial munido do seu produto interno usual e seja um operador linear simétrico cujo polinômio característico é . Se
, e ,
Então é igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 23
Q4. Denote por o operador identidade de e seja o operador linear tal que:
e .
Temos que é igual a:
a)
b)
c)
d)
e) .
Ver solução completaQuestão 24
Q12. Considere o espaço vetorial munido do seu produto interno usual e seja o operador linear simétrico cujos autovalores são 1 e -2 e que satisfaz
Em que denota o operador identidade de . Se , então é igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 25
Q13. O polinômio característico da matriz
É . Temos que a solução do sistema de equações diferenciais satisfazendo a condição é dada por:
- ;
- ;
Questão 26
Q10. Sejam um espaço vetorial real de dimensão finita munido de um produto interno e um operador linear. Suponha que exista uma base de tal que a matriz seja simétrica. Considere as seguintes afirmações:
(i) o operador é simétrico;
(ii) o operador é diagonalizável;
(iii) existe uma base ortonormal de formada por autovetores de .
Assinale a alternativa correta:
a) apenas as afirmações (i) e (ii) são necessariamente verdadeiras;
b) apenas a afirmação (i) é necessariamente verdadeira;
c) nenhuma das afirmações é necessariamente verdadeira;
d) apenas a afirmação (ii) é necessariamente verdadeira;
e) apenas as afirmações (ii) e (iii) são necessariamente verdadeiras.
Ver solução completaQuestão 27
Q14. Sejam e seja o operador linear tal que
Em que can denota a base canônica de . Temos que o subespaço
É invariante por se, e somente se:
a) e
b) e
c) e
d) e
e) e
Ver solução completaQuestão 28
Q11. Sejam um espaço vetorial complexo de dimensão finita e um operador linear. Considere as seguintes afirmações:
(i) se existir uma base de tal que a matriz seja real, então o polinômio característico de terá coeficientes reais;
(ii) se existirem tais que e o polinômio característico de seja então será diagonalizável;
(iii) se for um autovalor de , então também será um autovalor de .
Assinale a alternativa correta:
a) todas as afirmações são necessariamente verdadeiras;
b) apenas as afirmações (i) e (iii) são necessariamente verdadeiras;
c) apenas a afirmação (ii) é necessariamente verdadeira;
d) apenas as afirmações (i) e (ii) são necessariamente verdadeiras;
e) apenas a afirmação (i) é necessariamente verdadeira.
Ver solução completaQuestão 29
Q1. Sejam um espaço vetorial real de dimensão 3 munido de um produto interno e uma base de tal que:
e .
Se for a base ortogonal de obtida de pela aplicação do processo de ortogonalização de Gram-Schmidt, então será igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 30
Q11. Seja uma matriz cujos únicos autovalores reais sejam 1 e 3. Pode-se afirmar que:
a) é simétrica;
b) é diagonalizável sobre ;
c) o polinômio característico de é
d) a soma das entradas na diagonal principal de é igual a 4;
e) é inversível.
Ver solução completaQuestão 31
Q15. Considere o espaço vetorial munido do seu produto interno usual e seja o subespaço de definido por:
e .
Assinale a alternativa correspondente a uma base de :
a)
b)
c)
d)
e)
Ver solução completaQuestão 32
Q3. Sejam um espaço vetorial de dimensão finita munido de um produto interno, uma base de , um operador linear e . Assinale a alternativa correta:
a) se for simétrico e for ortonormal, então será diagonal;
b) se for simétrico e não for simétrica, então não será ortonormal;
c) se for ortonormal, então será simétrica e será diagonalizável;
d) se for diagonal, então será formada por autovetores de e será simétrico;
e) se for diagonalizável e for diagonal, então será ortonormal.
Ver solução completaQuestão 33
Q7. Considere o espaço vetorial munido do produto interno definido por:
Seja um operador linear simétrico cujos únicos autovalores sejam 2 e 5 e que satisfaça a igualdade
Em que denota o operador identidade de . Temos que é igual a:
Ver solução completaQuestão 34
Q9. Seja um espaço vetorial real de dimensão finita munido de um produto interno e considere as seguintes afirmações:
(i) se for uma base de e for ortogonal a todo elemento de , então
(ii) se for um subespaço de tal que , então
(iii) se for um operador linear e for um subespaço de invariante por , então também será invariante por .
Assinale a alternativa correta:
a) apenas a afirmação (ii) é necessariamente verdadeira;
b) apenas as afirmações (i) e (ii) são necessariamente verdadeiras;
c) apenas a afirmação (i) é necessariamente verdadeira;
d) todas as afirmações são necessariamente verdadeiras;
e) apenas as afirmações (i) e (ii) são necessariamente verdadeiras.
Ver solução completaQuestão 35
Seja o espaço vetorial de todas as funções e seja o subespaço de definido por
em que
para todo . Uma base para é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 36
Sejam um espaço vetorial de dimensão finita, e subespaços de e e bases de e , respectivamente. Considere as seguintes afirmações:
o conjunto é uma base de ;
existe uma base de que contém o conjunto
existe uma base de que contém o conjunto .
Assinale a alternativa correta:
a) apenas as afirmações e são necessariamente verdadeiras;
b) apenas as afirmações e são necessariamente verdadeiras;
c) apenas a afirmação é necessariamente verdadeira;
d) nenhuma das afirmações é necessariamente verdadeira;
e) apenas a afirmação é necessariamente verdadeira.
Ver solução completaQuestão 38
11. Seja um espaço vetorial real de dimensão finita munido de um produto interno, seja um operador linear e sejam , e autovalores de dois a dois distintos. Para cada , denote . Considere as seguintes afirmações:
I. Se e , então é simétrico.
II. Se é simétrico, então e .
III. Se é diagonalizável, , , são os únicos autovalores de e valem as inclusões e , então é simétrico.
Está correto o que se afirma em
(A) II e III, apenas.
(B) I, II e III.
(C) I e III, apenas.
(D) II, apenas.
(E) I, apenas.
Ver solução completaQuestão 39
12. Em , com o produto interno usual, seja um operador linear cujos autovalores distintos são , e e que satisfaz e . Considere as seguintes afirmações:
I. certamente não é simétrico.
II. Se é simétrico, então existem tais que com .
III. certamente é diagonalizável, e existem tais que com .
Está correto apenas o que se afirma em:
(A) II.
(B) II e III.
(C) I.
(D) I e III.
(E) III.
Ver solução completaQuestão 40
Q13. Seja um operador linear, em que é um espaço vetorial de dimensão 7. Considere as seguintes afirmações:
(i) se 4 for um autovalor de com multiplicidade algébrica igual a 3, então existirá um subconjunto linearmente independente de com três elementos tal que , e ;
(ii) se todas as raízes complexas do polinômio característico de forem reais, então a soma das multiplicidades geométricas dos autovalores de será igual a 7;
(iii) se 20, 30 e 40 forem autovalores de T, a multiplicidade geométrica do autovalor 20 for igual a 3 e a multiplicidade algébrica do autovalor 30 for igual a 3, então a multiplicidade geométrica do autovalor 40 será igual a 1.
Assinale a alternativa correta:
a) apenas as afirmações (ii) e (iii) são necessariamente verdadeiras;
b) apenas as afirmações (i) e (iii) são necessariamente verdadeiras;
c) apenas a afirmação (ii) é necessariamente verdadeira;
d) apenas a afirmação (iii) é necessariamente verdadeira;
e) nenhuma das afirmações é necessariamente verdadeira.
Ver solução completaQuestão 41
Seja um espaço vetorial e considere as seguintes afirmações:
- Se para todo inteiro existe um subconjunto linearmente independente de com elementos, então nenhum subconjunto finito de gera ;
- Se e são subespaços de tais que e se , são tais que
- Se e são subespaços de tais que é um subespaço de , então está contido em ou está contido em .
então e ;
Assinale a alternativa correta:
- apenas a afirmação (I) é necessariamente verdadeira;
- todas as afirmações são necessariamente verdadeiras;
- apenas as afirmações (I) e (III) são necessariamente verdadeiras;
- apenas as afirmações (I) e (II) são necessariamente verdadeiras;
- apenas as afirmações (II) e (III) são necessariamente verdadeiras.
Questão 42
Sejam A,B,C,D os pontos de definidos por . A altura do tetraedro ABCD relativa à base ABC é igual a:
Ver solução completa
Questão 44
Q4. Seja um espaço vetorial munido de um produto interno e sejam subespaços de tais que . Considere as seguintes afirmações:
(I) a soma é direta;
(II)
(III) é igual ao vetor nulo de , para todo .
Assinale a alternativa correta:
(a) Todas as afirmações são verdadeiras.
(b) Apenas a afirmação (II) é verdadeira.
(c) Apenas as afirmações (I) e (III) são verdadeiras.
(d) Apenas a afirmação (I) é verdadeira.
(e) Apenas a afirmação (III) é verdadeira.
Ver solução completaQuestão 45
Considere o espaço vetorial de todas as funções contínuas de e o subespaço S de
gerado pelas funções:
Temos que a dimensão de é igual a:
Questão 46
Sejam um espaço vetorial de dimensão munido de um produto interno
uma base de . Suponha que:
Se são tais que é a projeção ortogonal de sobre o subespaço , então é igual a:
Questão 47
Considere os subespaços do espaço vetorial definidos por:
em que denota a transposta de uma matriz . Temos que é igual a:
Questão 48
Considere os subespaços do espaço vetorial definidos por:
Temos que é igual a:
Questão 49
Sejam subespaços do espaço vetorial
em que
e é o conjunto solução do sistema linear homogêneo:
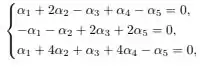
nas incógnitas reais . Assinale a alternativa correta:
(a) é um subespaço de
(b)
(c) .
(d)
(e)
Ver solução completaQuestão 50
Considere o espaço vetorial munido do produto interno definido por
para quaisquer . Se são tais que é uma base ortogonal de , então é igual a:
Questão 51
Seja um espaço vetorial de dimensão finita munido de um produto interno e denote por
a norma correspondente. Considere as seguintes afirmações:
(I) se são subespaços de , então ;
(II) para quaisquer , vale que se, e somente se, são linearmente
dependentes;
(III) se e se são dois a dois ortogonais e não nulos, então é igual a .
Assinale a alternativa correta:
(a) Apenas as afirmações (I) e (III) são verdadeiras.
(b) Todas as afirmações são verdadeiras.
(c) Apenas as afirmações (I) e (II) são verdadeiras.
(d) Apenas a afirmação (I) é verdadeira.
(e) Apenas a afirmação (III) é verdadeira.
Ver solução completaQuestão 52
Qual das afirmações abaixo é verdadeira:
- Em um conjunto de vetores é LD se não for gerador.
- Em ,um conjunto com 25 vetores é necessariamente LI.
- Em , um conjunto com 83 vetores pode ser gerador e não se LI.
- Em um conjunto com vetores é necessariamente gerador.
Questão 53
Sejam um espaço vetorial de dimensão e
bases de tais que:
Se é a transformação linear tal que
![]()
então os autovalores de são iguais a:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 54
Considere as seguintes afirmações:
(I) se é uma matriz real quadrada é diagonalizável e se existe um inteiro positivo tal que , então ;
(II) se é a transformação linear definida por
para todo e se , em que , então ;
(III) se é a transformação linear definida por para todo , então é diagonalizável.
Assinale a alternativa correta:
(a) apenas as afirmações (I) e (II) são verdadeiras
(b) todas as afirmações são verdadeiras
(c) apenas as afirmações (I) e (III) são verdadeiras
(d) apenas a afirmação (I) é verdadeira
(e) apenas a afirmação (III) é verdadeira
Ver solução completa