Nos exercícios 5-8, é dada a matriz de adjacência de um serviço de busca na Internet. Use o método do Exemplo 3 para ordenar os sites em ordem decrescente de autoridade.
6.
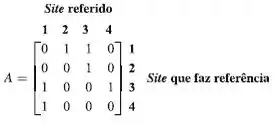
Passo 1
ALEERTAAAA: as contas pra esse capítulo são desumanas e praticamente impossíveis, então vamos usar alguma ferramente poderosa, como o excel para fazer os cálculos.
A matriz é:
E a sua transposta:
O vetor normalizado das somas das linhas da transposta:
Passo 2
Pra achar os vetores autoridade:
Passo 3
Respira um pouco e continua...
Daí podemos concluir que 1 e 3 estão empatados na frente e que 2 e 4 estão empatado atrás.
Resposta
2 e 4