Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 7.2 - Ex. 8
Nos Exercícios 2–9, encontre uma matriz que diagonaliza ortogonalmente e determine .
Passo 1
E aí? Bora matar essa questão?
Bom, precisamos encontrar a matriz que diagonaliza e , mas o que é isso?
Então, é uma matriz ortogonal formado pelos autovetores normalizados em coluna.
Relaxa que mais para frente eu conto como determinamos o autovetor normalizado, primeiro vamos ver a matriz :
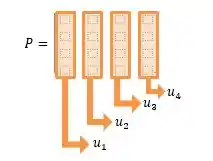
Agora, o que é , é a multiplicação das matrizes.
Foco no que eu disse ali em cima, sobre ser uma matriz ortogonal, então temos que:
Passo 2
Precisamos dos os autovalores e autovetores:
Passo 3
A primeira coisa que vamos fazer é calcular o autovalor:
E vamos fazer parte, primeiro :
Passo 4
Lembra da equação que escrevemos ali em cima?
Agora vamos substituir os valores nela:
Reescrevendo:
Então:
Passo 5
Bora fazer o determinante da nossa matriz?
Vamos calcular os cofatores:
Bora resolver a matriz:
Passo 6
Retornando para:
Relembrando:
Logo:
Colocando em evidência:
Temos:
Passo 7
Agora é a vez dos autovetores:
Onde:
Logo:
Como já temos :
Vamos substituir os valores encontrados dos autovalores para determinar . Molezinha, não!?
Passo 8
Para :
Montando em forma de sistema, temos:
Agora só escolher uma equação do sistema, não importa qual. Vamos escolher:
O objetivo é isolar uma das incógnitas, que tal escolhermos o :
Substituindo em:
Substituindo em :
E temos:
Escrevendo:
E:
Passo 9
Para :
Montando em forma de sistema, temos:
Agora só escolher uma equação do sistema, não importa qual. Eu vamos escolher a primeira:
O objetivo é isolar uma das incógnitas, que tal escolhermos o :
Falta saber os valores de e .
Para , usamos a terceira equação:
Para z, usamos a terceira equação:
Escrevendo:
Colocando em evidência, temos:
Temos que o valor de autovetor é:
Passo 10
Para :
Montando em forma de sistema, temos:
Agora só escolher uma equação do sistema, não importa qual. Eu vamos escolher a primeira:
O objetivo é isolar uma das incógnitas, que tal escolhermos o :
Falta saber os valores de e .
Para , usamos a terceira equação:
Para z, usamos a terceira equação:
Escrevendo:
Colocando em evidência, temos:
Temos que o valor de autovetor é:
Passo 11
Estamos mandando bem!!! Bora determinar normalizar os autovetores:
Passo 12
Não desiste de mim, que falta pouco!!!
Bora escrever, !?
Para escrever , lembra o que eu disse lá no Passo 1? Que colocamos os autovetores normalizados que diagonaliza ortogonalmente em colunas, então:
Passo 13
Estamos quase no fim, eu juro!!!
Agora vamos determinar , para isso vamos transformar na matriz identidade.
Primeiro vamos escrever:
Se liga na anotação que vamos usar para simbolizar nossas operações (utilizando como exemplo nossa primeira operação, vamos inverter duas linhas:
Fazendo:
Fazendo:
Fazendo:
Fazendo:
Fazendo:
Passo 14
Último passo antes da tão sonhada !!!!
Só precisamos fazer substituir:
Passo 15
Bora fazer com a nossa multiplicação!!!
Mandamos bem!!! Partiu, outra questão?