Ache o polinômio característico, os autovalores e os autovetores de cada matriz:

f)

Para isso precisamos calcular o determinante da seguinte matriz:

E igualar a zero, temos:

Beleza, as raízes deste polinômio, serão os nossos autovalores! Bora lá!

Para encontrar as raízes deste polinômio pode ser um pouco chato (se puder, faça computacionalmente), mas vamos aqui, tentar aplicar o método de Briot-Ruffini para diminuir o grau deste polinômio através de uma raiz conhecida e então teremos um polinômio de segundo grau como usualmente. Existem vários materiais no site com mais detalhes sobre o método, mas para esta questão podemos resumi-lo da seguinte forma:

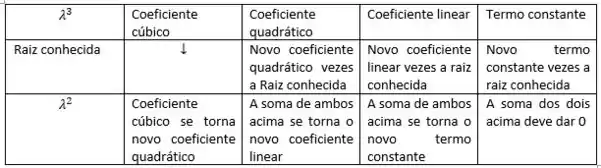
Mas antes disso, precisamos encontrar ao menos 1 raiz! Vamos lá!

A maneira mais conveniente de fazer isso é chutando valores utilizando de certos critérios! O principal seria analisar o termo constante no polinômio característico, ou seja, -8, e testar os valores do qual este termo é múltiplo, sendo estes:

Precisamos aplicar todas elas em nosso polinômio característico (1), e ver se alguma delas é uma raiz! Faça o teste um a um se precisar, aqui vou apenas apresentar a que dá certo, beleza? No caso, temos que . Saca só!

Belezinha, temos nossa primeira raiz! Vamos aplicar o método de redução de ordem!

Aplicando o procedimento que descrevi acima, utilizando a raiz conhecida , temos:

Portanto, temos que, o nosso polinômio reduzido é tal que

Agora podemos aplicar Bhaskara para encontrar o restante de nossas raízes! Vamos lá!

Aplicando Bhaskara, temos:

E para a segunda raiz, temos:

Temos então todos os nossos autovalores, sendo eles , e e . Vamos achar os autovetores!

Para encontrar os autovetores temos que aplicar cada uma de nossas raízes individualmente na definição:

Vamos começar com , temos:

Realizando o produto matricial, temos:

Temos aqui um sistema linear para os parâmetros do autovetor, vamos escalonar a matriz dos coeficientes para obter o resultado, tudo bem?

Primeiro passo é escrever nossa matriz como:

Para criar o pivô, divida a primeira linha por 3, temos:

Agora, para eliminar o restante da coluna do pivô, subtraia a primeira linha da segunda e também subtraia 2 vezes a primeira linha da terceira, obtendo:

Agora, vamos seguir deixando o próximo termo diagonal igual a 1, temos que multiplicar a segunda linha por ¾, temos:

Para eliminar o restante da segunda coluna vamos subtrair a 3/2 da segunda linha da primeira, e somar 3/10 da segunda linha na terceira, obtendo:

Temos então que a solução do nosso sistema é tal que:

e

Nosso primeiro vetor então é da forma , em é um valor real qualquer. Vamos achar nosso segundo autovetor!

Agora com , temos:

Realizando o produto matricial, temos:

Temos aqui um sistema linear para os parâmetros do autovetor, vamos escalonar a matriz dos coeficientes para obter o resultado, tudo bem?

Primeiro passo é escrever nossa matriz como:

Para criar o pivô, vamos trocar a segunda linha com a primeira, temos

Agora, para eliminar o restante da coluna do pivô, subtraia duas vezes a primeira linha da terceira, obtendo:

Agora, vamos seguir deixando o próximo termo diagonal igual a 1, temos que dividir a segunda linha por 2:

Para eliminar o restante da segunda coluna vamos somar a 2 vezes a segunda linha na terceira obtendo:

Temos então que a solução do nosso sistema é tal que:

e

Nosso segundo vetor então é da forma , em é um valor real qualquer. Vamos achar o nosso último autovetor!

Usando , temos:

Realizando o produto matricial, temos:

Temos aqui um sistema linear para os parâmetros do autovetor, vamos escalonar a matriz dos coeficientes para obter o resultado, tudo bem?

Primeiro passo é escrever nossa matriz como:

Para criar o pivô, divida a primeira linha por -2, temos:

Agora, para eliminar o restante da coluna do pivô, subtraia a primeira linha da segunda e também subtraia 2 vezes a primeira linha da terceira, obtendo:

Agora, vamos seguir deixando o próximo termo diagonal igual a 1, temos que multiplicar a segunda linha por -1, temos:

Para eliminar o restante da segunda coluna vamos somar a segunda linha na primeira, temos:

Temos então que a solução do nosso sistema é tal que:

e

Nosso último vetor então é da forma , em é um valor real qualquer. Com esse último autovetor, acabamos a questão! É isso aí! Te vejo na próxima! Tchau Tchau