Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 30
Na Fig. 9-3, a circunferência de centro tem raio . Calcule em função de e das medidas e dos ângulos indicados. Aplique o resultado para provar que todo ângulo inscrito em uma circunferência é reto.
Passo 1
O primeiro passo para facilitar esse problema é definir uma base ortonormal com os eixos e , mostrados na figura:
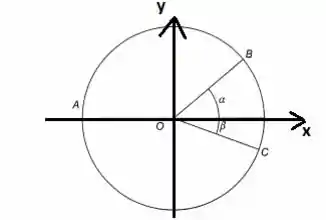
Vamos escrever as coordenadas de cada ponto:
Assim,
Da mesma forma,
Logo,
Passo 2
Fazendo o produto escalar desses vetores:
Assim,
Ou ainda,
Como e , temos que
Ou ainda,
Passo 3
Caso o ângulo seja inscrito em uma semicircunferência, temos que , de modo que
Portanto, é ortogonal a e o ângulo é reto!
Resposta
Exercícios de Livros Relacionados
Prove que, se a matriz M é ortogonal, então det M = 1 ou det M = - 1 . Vale a recíproca?
Sabendo que u → + v → + w → = 0 → , u → = 3 / 2 , v → = 1 / 2 e w → = 2 , calcule u → ⋅ v → + v → ⋅ w → + w → ⋅ u → .
Sendo u → e v → unitários, w → = 4 , u → ⋅ w → = - 2 , v → ⋅ w → = - 4 , e a n gu → ,v → = π / 3 , calcule: 5 u → - w → ⋅ ( w → - 2 u → )
Calcule 2 u → + 4 v → 2 , sabendo que u → é unitário, v → = 2 , e a medida angular entre u → e v → é 2 π / 3 radianos.
Sendo u → e v → unitários, w → = 4 , u → ⋅ w → = - 2 , v → ⋅ w → = - 4 , e a n gu → ,v → = π / 3 , calcule: w → - v → + u → ⋅ ( - u → + 2 w → + v → )