Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 39
Prove que:
a)
b) as diagonais de um paralelogramo são perpendiculares se, e somente se, o paralelogramo é um losango.
c) é ortogonal a
Passo 1
O item (a) é bem simples e serve de guia para demonstrar o item (b). Fazendo a distributiva:
Os termos mistos se cancelam, restando
Lembre-se que .
Passo 2
No item (b) temos que considerar a figura:
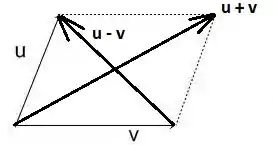
As diagonais do paralelogramo são dadas por e . Sabemos que elas são perpendiculares se, e somente se,
Nesse caso, pelo item (a), temos que
Neste caso, todos os lados do paralelogramo são iguais e ele é chamado de losango. Provamos o item (b)!
Passo 3
No item (c), queremos mostrar que é ortogonal a . Para isso, basta fazer o produto escalar:
Os termos do meio se cancelam, de modo que
Portanto, eles são ortogonais!
Resposta
Demonstração.
Exercícios de Livros Relacionados
Decomponha u → = ( 1 ,0 ,3 ) como soma dos vetores v → e w → tais que v → , ( 1 ,1 ,1 ) e ( - 1 ,1 ,2 ) sejam LD e w → seja ortogonal aos dois últimos.
Obtenha u → ortogonal a ( 1 ,1 ,0 ) tal que u → = 2 e a medida angular em graus entre u → e ( 1 ,- 1 ,0 ) seja 45 ° .
a) Obtenha os vetores de norma 3 3 que são ortogonais a u → = ( 2 ,3 ,- 1 ) e a v → = ( 2 ,- 4 ,6 ) .b) Qual dos vetores obtidos no item (a) forma ângulo agudo com ( 1 ,0 ,0 ) ?
Descreva o conjunto de todos os vetores w → ortogonais a v → = ( 2 ,1 ,2 ) tais que u → = ( 1 ,1 ,- 1 ) seja combinação linear de v → , w → .
Dados v → = ( 1 ,1 ,1 ) , w → = 0 ,1 ,- 1 e t → = ( 2 ,1 ,- 1 ) , obtenha u → de norma de 5 , ortogonal a t → , tal que ( u → ,v → ,w → ) seja LD.