Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 10

No hexágono A B C D E F temos A B   → = 2   a →   , F C   → = 7   a →   , E D   → =   3 a →   e B C   → = F E →   =   b →   . Expresse v →   =   C S → como combinação linear de a → e b → , sabendo que A S   → / /   B C → .

Passo 1

Fala, galera! Tudo tranquilo?

Vamos, primeiramente, processar as informações do enunciado: A B   → = 2   a →   , F C   → = 7   a →   , E D   → =   3 a →   e B C   → = F E →   =   b →   . Usando essas informações, obtemos a figura do livro:

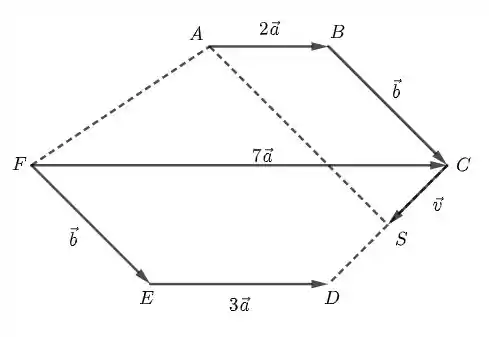
Queremos que A S   → / /   B C → = b → , então

A S   → = λ B C → = λ b →

Por outro lado,

A S   → = A B   → + B C   → + C S   → = 2   a →   +   b → + v →  

Logo,

A S   → = 2   a →   +   b → + v → = λ b →

Passo 2

Agora, temos que tentar escrever v →   =   C S → em termos de a → e b → . Sabemos que C S   → / /   C D → , então

v → = C S   → = α   C D → = α ( C F → + F E → + E D → ) = α ( - F C → + F E → + E D → ) = α ( - 7   a → +   b → + 3 a → )

v → = α ( - 4 a → +   b → )

Podemos então substituir v →   =   C S → em A S   → para determinar o parâmetro α :

A S   → = 2   a →   +   b → + v → = 2   a →   +   b → + α ( - 4 a → +   b → ) = λ b → ⇒ ( 2 - 4 α ) a → + ( 1 + α ) b → = λ b →

( 1 + α - λ ) b → = ( 4 α - 2 ) a →

Como vocês já sabem, a equação acima só é verdadeira quando ambos os lados são nulos, uma vez que a → e b → são l.i. Assim,

1 + α - λ = 0 ⇒ α = λ - 1

4 α - 2 = 0 ⇒ α = 1 2

Não precisamos determinar λ , apenas α . Com isso, substituindo α = 1 2 em v → , obtemos:

v → = α ( - 4 a → +   b → ) = 1 2 ( - 4 a → +   b → ) = - 2 a → + 1 2   b → .

Resposta

v → = - 2 a → + 1 2   b →

Exercícios de Livros Relacionados

A figura ao lado é um cubo e B = ( a → , b → , c → ) é uma base.(a)Demonstre, algebricamente, que C = ( A G → , A F → , A H → ) é uma base.
A figura ao lado é um cubo e B = ( a → , b → , c → ) é uma base.(b)Determine na base B as coordenadas de x → = 1,2 , - 2 C .
Dados os vetores u e v, prove que as afirmações seguintes são equivalentes: b) Se αu + βv = α′u + β′v então α = α′ e β = β′.
Dados os vetores u e v, prove que as afirmações seguintes são equivalentes: a) Uma combinação linear αu + βv só pode ser igual a zero quando α = β = 0.
Seja P um ponto interior ao triangulo ABC tal que P A → + P B → + P C → = 0 . Prove que as retas AP, BP e CP são medianas de ABC, logo P é o baricentro desse triângulo.