Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 6k
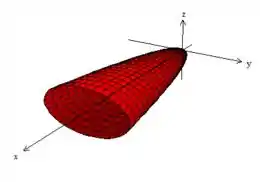
6. Identificar e representar graficamente as superfícies expressas pelas equações nos intervalos dados.
Passo 1
Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:
POXA! O primo dessa equação, , não é uma parábola ao redor de ? Então... é um... PARABOLOIDE ELÍPTICO e também ao redor de . O desenho dela no espaço será mais ou menos assim, óh:
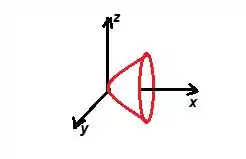
OBSERVAÇÃO: Essa ainda não é a representação gráfica da nossa equação e sim apenas um esboço de quem ela vai ser ok? Se quiser ver como se desenha perfeitamente essa quádrica, venha comigo para o próximo passo!
Passo 2
- Primeiro repare que só queremos a parte que vai até (já o exercício nos impôs a condição de que ).
- Segundo, repare que em cima do plano , a equação nos dará...
OPA! Essa equação nos representa o quê? SIM! Uma elipse de eixo maior em !
Com essas informações, e tendo em mente o nosso esboço do passo 1, podemos finalmente desenhar a nossa quádrica:
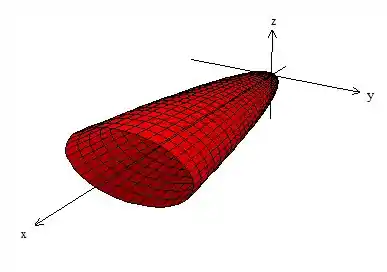
Viu só!
Resposta
Paraboloide Elíptico.
