Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 8d
8. Identificar a superfície e a sua interseção com o plano dado. Representar graficamente esta interseção no plano .
Passo 1
FALÁ! Tudo bom, contigo?
Bem, eu não sei se você reparou, mas essa equação que o problema nos pede para identificar... Hmmmm! Não sei não, heim? Mas ela me parece com a equação de um hiperbolóide!
Será que é verdade isso? Venha comigo para você saber .
Passo 2
Bem! Sabemos que a equação de um hiperbolóide tem que ser algo do tipo:
A nossa equação é assim:
ORA! Da teoria do nosso livro, se temos uma sequência de sinais do tipo , então é porque estamos lidando com um hiperboloide de duas folhas!
Passo 3
Para encontrar a tal da intersecção com o nosso plano , basta resolver o sistema:
Substituindo na equação de ...
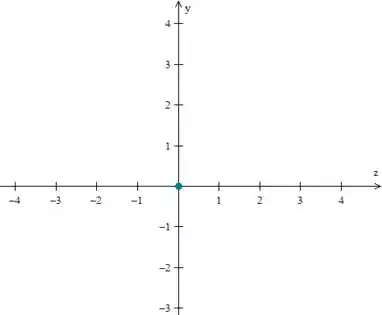
OPA! O único valor possível para a solução dessa equação é se for e também for ! Portanto, no plano a solução da intercecção do plano com a superfície é um ponto: a origem...
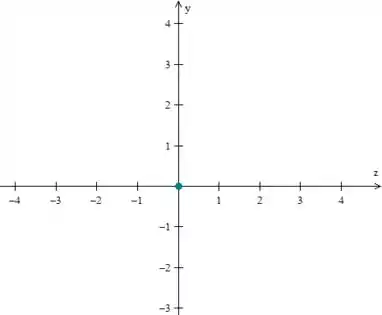
Resposta
Equação representa um hiperboloide de duas folhas. Intersecção é um ponto (a origem):
