Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 9.Problemas propostos - Ex. 7l
7. Identificar as superfícies definidas pelas equações, dizendo ao longo de que eixo elas ocorrem, conforme o caso.
Passo 1
Fala aí! Nesse exercício daqui estaremos trabalhando a seguinte equação:
Essa equação, a gente já a viu antes e ela representa a equação de um plano, não é mesmo?
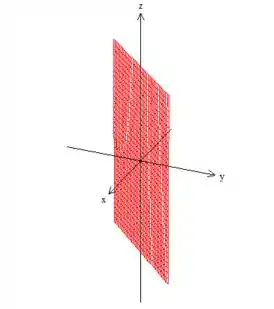
Bem, sim e não ao mesmo tempo: do ponto de vista geométrico somente é um plano, mas do pode de vista da geometria analítica... Essa equação representa um cilindro, afinal de contas não tem uma das variáveis (a variável ). Vamos ver isso melhor então.
Passo 2
No plano , essa equação é uma reta:
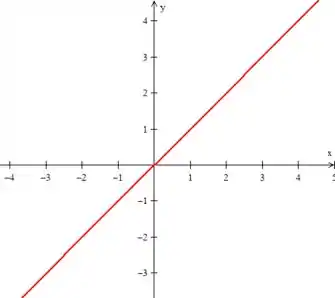
Como falta a variável , podemos puxar essa reta para cima (translada-la) ao redor do eixo :
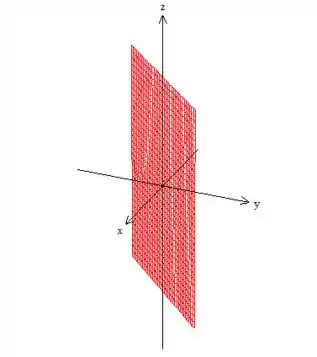
Então está aí! Um cilindro ao redor do eixo e de diretriz sendo uma reta. Em outras palavras, um plano .
Resposta
Cilindro ao redor de de diretriz sendo uma reta:
