Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Reginaldo - Matrizes, Vetores e Geometria Analítica- Ed: 1º - Capítulo 7.2 - Ex. 11

Identifique a cônica, ache a equação no ultimo sistema de coordenadas utilizado e faça um esboço do gráfico. 8 x 2 - 16 x y + 8 y 2 + 33 2 x - 31 2 y = - 70

Passo 1

Fala aeee, tudo na paz? 😊

Da equação da cônica tiramos que:

a = 8

b =   - 16

c = 8

e = 33 2

f =   - 31 2

Portanto:

A =   a b 2 b 2 c = 8 - 8 - 8 8

Passo 2

O polinômio característico será dado por:

P λ = det ⁡ A - λ I 2 = 8 - λ - 8 - 8 8 - λ = λ 2 - 16 λ

λ 2 - 16 λ = 0

Temos como raízes do polinômio:

λ 1 = 0

λ 2 = 16

Passo 3

Para determinarmos os vetores U   e   T .

Precisamos que:

A - 0 I 2 X   = 0 →

8 - 8 - 8 8 x y = 0 0

8 x - 8 y = 0

x = y

Solução Geral:

W = α , α ; α ∈ R

Passo 4

Como a norma de w vale 1:

W = 1

W 2 = 1

α 2 + α 2 = 1

α =   ± 1 2

Assim, os eixos deslocados são expressos por:

U = 1 2 , 1 2

T = ( - 1 2 , 1 2 )

P = U , T = 1 2 - 1 2 1 2 1 2

Passo 5

e , f   x   P =   e 1 , f 1

33 2 - 31 2 x 1 2 - 1 2 1 2 1 2 = e 1 , f 1

e 1 , f 1 = [ 2 ,   - 64 ]

Agora que eliminamos o termo x y , podemos escrever a equação da nossa cônica:

∁ : 8 x 2 - 16 x y + 8 y 2 + 33 2 x - 31 2 y = - 70 →   λ 1 x 1 2 + λ 2 y 1   2 + e 1 x 1 + f 1 y 1 = - 70

∁ : 16 y 1   2 + 2 x 1 - 64 y 1 = - 70 ÷ - 70

∁ : - 8 35 y 1   2 + 32 35 y 1 = 1 35 x 1 + 1

Equação de uma parábola.

Passo 6

Gráfico da cônica:

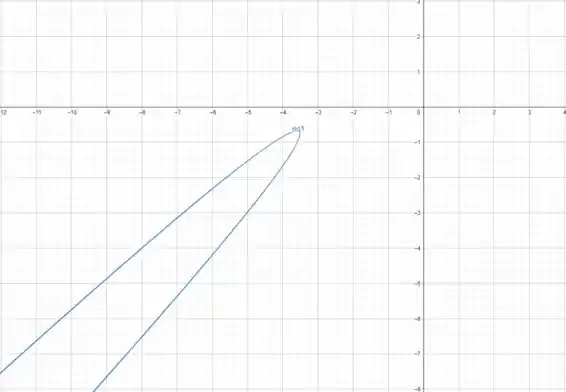
Resposta

∁ : - 8 35 y 1   2 + 32 35 y 1 = 1 35 x 1 + 1

Exercícios de Livros Relacionados

Identifique a cônica, ache a equação no ultimo sistema de coordenadas utilizado e faça um esboço do gráfico. 9 x 2 - 4 x y + 6 y 2 = 30
Identifique a cônica, ache a equação no ultimo sistema de coordenadas utilizado e faça um esboço do gráfico. 3 x 2 - 8 x y - 12 y 2 = - 81
Identifique a cônica, ache a equação no ultimo sistema de coordenadas utilizado e faça um esboço do gráfico. 2 x 2 - 4 x y - y 2 = - 24
Considere o polinômio p λ = det ⁡ A - λ I 2 , em que A =a b / 2 b / 2 c . e) Mostre que sempre existe um ângulo θ tal que R θ t A R θ =a ' 0 0 c ' e portanto tal que a mudança de coordenadas dada por
Identifique a cônica, ache a equação no ultimo sistema de coordenadas utilizado e faça um esboço do gráfico. 5 x 2 - 6 x y + 5 y 2 - 30 2 x + 1 8 2 y = - 82