Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 23.Exercício - Ex. 4efg

Identifique e esboce a cônica, conhecendo sua equação;

  1. 3 x 2 + 2 x y + 3 y 2 + 6 2 x + 2 2 y + 2 = 0 .
  2. x 2 + 4 y 2 + 3 3 x y - 1 = 0 .
  3. x 2 + 4 x y + 4 y 2 - 1 = 0 .
  4. 7 x 2 + 5 y 2 + 2 3 x y - 14 + 2 3 x - 10 + 2 3 y + 8 + 2 3 = 0 .
  5. 7 x 2 + 6 x y - y 2 + 28 x + 12 y + 28 = 0 .
  6. 16 x 2 - 108 x y - 29 y 2 + 260 = 0 .
  7. 5 x 2 + 2 y 2 + 2 x y + 2 = 0 .

Passo 1

(e) Para eliminar os termos lineares, montamos:

M 3 = a b / 2 d / 2 b / 2 c e / 2 d / 2 e / 2 f = 7 3 14 3 - 1 6 14 6 28

Assim, montamos o sistema

7 h + 3 k + 14 = 0 3 h - k + 6 = 0 ⟹ h = - 2   e   k = 0

Assim,

f ' = 14 h + 6 k + 28 = 14 - 2 + 6 ⋅ 0 + 28 = 0 ∴ f ' = 0

A equação fica

g x , y = 7 x 2 + 6 x y - y 2

Passo 2

Agora deveríamos fazer a rotação para eliminar o termo misto. Porém, note que podemos fazer uma simples fatoração:

7 x 2 + 6 x y - y 2 = 0 ⟺ 7 x 2 + 7 x y - x y - y 2 = 0 ⟺ 7 x x + y - y x + y = 0 ⟺

x + y 7 x - y = 0

Portanto, vemos que temos a reunião de duas retas: x + y = 0 e 7 x - y = 0 . No sistema x O y original (antes da translação), podemos verificar que as retas se encontram em h ,   k = - 2,0 , conforme mostra a figura abaixo.

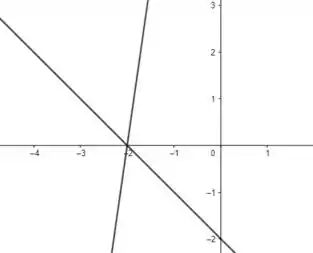
Passo 3

(f) Aqui, bastará fazer a rotação (já que não existe termos lineares). Assim,

cot ⁡ 2 θ = 16 + 29 108 = 5 12

Como

sin ⁡ 2 θ = 1 1 + cot 2 ⁡ 2 θ = 1 1 + 5 12 2 = 12 13

Assim, ficamos com o sistema

a ' + c ' = 16 + 29 = 45 a ' - c ' = - 108 12 / 13 ⟹ a ' + c ' = 45 a ' - c ' = - 117 ⟹ a ' = - 36   e   c ' = 81

A nova equação será

- 36 x 2 + 81 y 2 + 260 = 0 ⟹ 36 260 x 2 - 81 260 y 2 = 1

Que representa uma hipérbole.

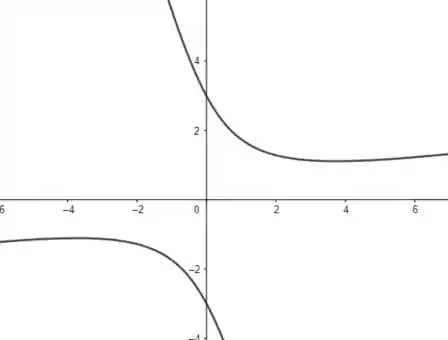
Passo 4

(g) Note que podemos escrever

5 x 2 + 2 y 2 + 2 x y + 2 = 0 ⟺

x 2 + 2 x y + y 2 + 4 x 2 + y 2 + 2 = 0 ⟺

x + y 2 + 4 x 2 + y 2 + 2 = 0

Porém, note que x + y 2 ≥ 0 , 4 x 2 ≥ 0 e y 2 ≥ 0 .

x + y 2 + 4 x 2 + y 2 ≥ 0 + 0 + 0 = 0

x + y 2 + 4 x 2 + y 2 ≥ 0

Adicionando 2 em ambos lados da desigualdade

x + y 2 + 4 x 2 + y 2 + 2 ≥ 2 > 0

mostrando que é impossível a igualdade x + y 2 + 4 x 2 + y 2 + 2 = 0 . Logo, a cônica dada é, na verdade, o conjunto vazio.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada parte, encontre a matriz canônica do operador matricial dado. a) T:R 3→R 3 reflete cada vetor no plano x z e, em seguida,contrai esse vetor pelo fator k = 1 5 .
em cada parte, use o Teorema 4.10.2 para determinar se T:R 2→R 2 é um operador matricial.b) T x , y = ( x + 1 , y ) .
em cada parte, use o Teorema 4.10.2 para determinar se T:R 2→R 2 é um operador matricial.b) T x , y = ( x 2 , y ) .
em cada parte, use o Teorema 4.10.2 para determinar se T:R 3→R 2 é um operador matricial.b) T x , y = ( 3 x - 4 y , 2 x - 5 z ) .
Em cada parte, encontre a matriz canônica do operador matricial dado. b) T:R 3→R 3 projeta cada vetor ortogonalmente sobre o plano x z e, em seguida, projeta esse vetor ortogonalmente sobre o plano x