Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 38

Utilizando as informações dadas em cada caso, calcule a excentricidade da elipse E . Aponte, entre elas, quais são semelhantes, qual é a mais alongada e qual é a menos alongada.

  1. E : 16 x 2 + 25 y 2 = 400 .
  2. A coroa fundamental de E tem raios 5 e 10.
  3. E : 2 x 2 + y 2 - 50 = 0 ;
  4. O triângulo F 1 B 2 F 2 é retângulo.
  5. As diagonais do retângulo fundamental de E formam ângulos de 60 ° .
  6. A área do retângulo fundamental é 8 , e a da coroa fundamental é 3 π .

Passo 1

  1. Dividindo ambos os membros por 400:

    2. 16 400 x 2 + 25 400 y 2 = 1 ⟹ x 2 25 + y 2 16 = 1

    onde identificamos que a 2 = 25 , b 2 = 16 . Logo

    c 2 = a 2 - b 2 = 9 ⟹ c = 3

    A excentricidade será:

    e = c a = 3 5

    Passo 2

  2. A coroa fundamental de uma elipse possui raio interno b e raio externo a . Portanto, segue que b = 5 e a = 10 . Portanto, c 2 = a 2 - b 2 = 75 ∴ c = 5 3 . A excentricidade será:

    3. e = c a = 5 3 10 = 3 2

    Passo 3

  3. Podemos fazer:

    4. 2 x 2 + y 2 - 50 = 0 ⟺

    2 x 2 + y 2 = 50 ⟺

    x 2 25 + y 2 50 = 1

    Assim, vemos que a 2 = 50 e b 2 = 25 . Segue:

    c 2 = a 2 - b 2 = 50 - 25 = 25 ⟹ c = 5

    Portanto, a excentricidade será:

    e = c a = 5 5 2 = 2 2

    Passo 4

  4. Veja a figura abaixo

    5. Seja O o centro da elipse. Pela simetria, vemos que O B 1 F 2 é um triângulo retângulo isósceles. Assim, B 1 O = b = O F 2 = c . Portanto,

    a 2 = b 2 + c 2 ∴ a 2 = c 2 + c 2 = 2 c 2 ⟹ a = 2 c

    Portanto,

    e = c a = c 2 c = 2 2

    Passo 5

  5. O retângulo fundamental possui lados a e b , conforme mostra a figura abaixo.

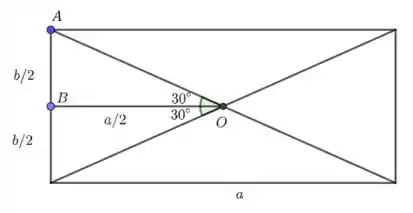
    6. No triângulo retângulo A B O , temos

    tan ⁡ 30 ° = b / 2 a / 2 ⟹ b = 1 3 a

    Logo,

    a 2 = b 2 + c 2 ∴ a 2 - 1 3 a 2 = c 2 ⟹ c 2 = 2 3 a 2 ∴ c = 2 3 a

    Segue que

    e = c a = 2 3

    Passo 6

  6. A área do retângulo fundamental é A = 2 a 2 b e da coroa fundamental é A = π a 2 - b 2 :

4 a b = 8 π a 2 - b 2 = 3 π ⟹ a b = 2 a 2 - b 2 = 3

Da primeira equação, b = 2 / a , de modo que

a 2 - 4 a 2 = 3 ∴ a 4 - 3 a 2 - 4 = 0 ⟹ a 2 + 1 a 2 - 4 = 0

Como a 2 + 1 = 0 não é possível (já que a ∈ R ), segue que

a 2 - 4 = 0 ⟹ a 2 = 4 ∴ a = 2

(note que a > 0 , de modo que desprezamos a raiz negativa). Portanto,

b = 2 a ⟹ b = 1

Finalmente, c 2 = a 2 - b 2 = 3 ∴ c = 3 .

e = c a = 3 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva uma equação reduzida da elipse, nos casos:O centro é O , os focos estão em O x , o eixo menor mede 6, e a distância focal é 8.O centro é O , os focos estão em O y , o eixo maior mede 10, e a d
Mostre que:Dentre as cordas perpendiculares à reta focal, B 1 B 2 é a de maior comprimento, 2b;A amplitude focal da elipse é 2 b 2 / a .
Escreva uma equação reduzida da elipse, nos casos:O centro é O , os focos estão em O x , o eixo menor mede 6, e a distância focal é 8.O centro é O , os focos estão em O y , o eixo maior mede 10, e a d
Sejam E e a como na Definição 22 - 1 . Prove que:Os focos e o centro de E não pertencem a E ;Nenhum ponto do segmento focal de E pertence a E ;Existem precisamente dois pontos A 1 e A 2 da reta focal
Mostre que uma elipse fica determinada pelo seu retângulo fundamental, mas não por sua coroa fundamental. Em outras palavras: cada retângulo é retângulo fundamental de uma só elipse, mas várias elipse