Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 131
Imponha condições sobre e para que exista um quadrado de lados paralelos aos eixos coordenados com vértices na hipérbole , e calcule sua área.
Passo 1
Temos o seguinte esquema, onde é o lado do quadrado:
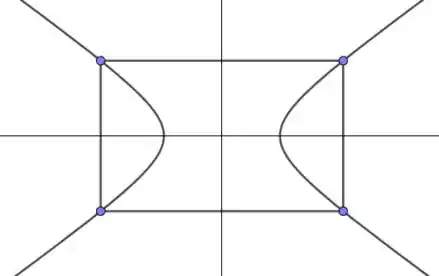
Sejam e os vértices do quadrado. Substituindo as coordenadas de quaisquer um dos vértices na equação da elipse, temos:
Passo 2
Notemos que a condição para que o quadrado existe é , pois caso contrário teremos um número negativo dentro da raiz.
Passo 3
A área do quadrado será:
Resposta
A condição é que . A área é
Exercícios de Livros Relacionados
Para as funções dadas f e g defina f - g e determine o domínio da função resultante. f x = x e g x = 1 x 2
Para as funções dadas f e g defina f ⋅ g e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3
Para as funções dadas f e g defina f ο g e determine o domínio da função resultante. f x = x 2 - 9 e g x = x + 5
Para as funções dadas f e g defina f + g e determine o domínio da função resultante. f x = x 2 - 9 e g x = x + 5
Para as funções dadas f e g defina f ο g e determine o domínio da função resultante. f x = x e g x = 1 x 2