Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 132

Sejam A e B , respectivamente, extremidades dos eixos maior e menor de uma elipse de centro O , F um dos focos e C um ponto da elipse tal que C F é perpendicular ao eixo maior.

  1. Supondo que O C → = k A B →   , exprima k em função da excentricidade da elipse.
  2. Supondo que O C → e A B → sejam paralelos, determine a excentricidade e mostre que o losango B 1 F 1 B 2 F 2 é um quadrado.

Passo 1

  1. Temos o seguinte esquema:

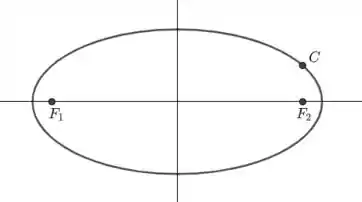
    Note que C deve possuir abscissa igual a c . Sua ordenada será:

    c 2 a 2 + y 2 b 2 = 1 ∴ e 2 + y 2 b 2 = 1 ∴ y = b 1 - e 2

    Logo, C = c ,   b 1 - e 2   .

    Passo 2

    Temos que

    O C → = x C 2 + y C 2 = c 2 + b 2 1 - e 2 = c 2 + a 2 - c 2 1 - e 2

    O C → = c 2 1 + a c 2 - 1 1 - e 2 = c 1 + 1 e 2 - 1 1 - e 2

    O C → = c e e 2 + 1 - e 2 2 = c e e 4 - e 2 + 1

    E

    A B → = a 2 + b 2 = a 2 + a 2 - c 2 = 2 a 2 - c 2 = c 2 e 2 - 1 = c e 2 - e 2

    Portanto,

    c e e 4 - e 2 + 1 = k ⋅ c e 2 - e 2 ⟹ k = e 4 - e 2 + 1 2 - e 2

    Passo 3

  2. Sendo O C → paralelo a A B → então existe k tal que

O C → = k ⋅ B A → ⟹ C - O = k A - B ∴ c , b 1 - e 2 = k a , 0 - 0 , - b

c ,   b 1 - e 2 = k a ,   b ⟹

Logo, vemos que

b ⋅ k = b 1 - e 2

Já calculamos o valor de k no item (a). Assim,

e 4 - e 2 + 1 2 - e 2 = 1 - e 2 ⟹ e 4 - e 2 + 1 = 1 - e 2 2 - e 2

e 4 - e 2 + 1 = 2 - 3 e 2 + e 4 ⟹ 2 e 2 = 1 ∴ e = 1 2

Passo 2

Assim, temos que

c a = e = 1 2 ⟹ a = 2 c       ∴       c 2 + b 2 = a 2 ⟹ c 2 + b 2 = 2 c 2 ⟹ b = c

Para que B 1 F 1 B 2 F 2 seja um quadrado, basta com que suas diagonais sejam iguais:

B 1 B 2 - = F 1 F 2 - ⟹ 2 b = 2 c ∴ b = c

o que já mostramos ser verdade.

Resposta

  1. k = e 4 - e 2 + 1 2 - e 2 .
  2. e = 1 / 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para as funções dadas f e g defina g ο f e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3
Para as funções dadas f e g defina f / g e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3
Para as funções dadas f e g defina f ⋅ g e determine o domínio da função resultante. f x = x e g x = 1 x 2
Para as funções dadas f e g defina f + g e determine o domínio da função resultante. f x = x 2 - 4 e g x = 4 x - 3
Para as funções dadas f e g defina f - g e determine o domínio da função resultante. f x = x + 2 e g x = x 2 + 4