Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 14.4 - Ex. 14
Numa indústria química há uma caldeira cuja margem de segurança é tal que a pressão é medida em atmosferas, e a temperatura , medida em graus Celsius, devem ser reguladas de maneira que . Quer-se usar a caldeira para que seja processada uma determinada reação. Para que isto ocorra da forma desejada, a temperatura deve estar entre e , e a pressão entre e atmosferas. A que temperatura e pressão deve trabalhar a caldeira para que a reação se processe no menor tempo possível, se sabemos que a velocidade da reação é dada por ?
Passo 1
O que a gente tem que fazer aqui é esboçar a região do plano que corresponde ao nosso problema, com todas as condições que ele deu. Vamos reunir todas?
E aí o nosso trabalho é desenhar essa região!
Passo 2
Esboçando:
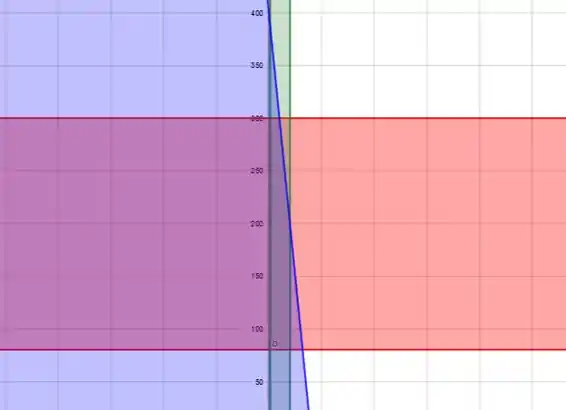
Aqui, considerei a pressão no eixo horizontal e a temperatura no eixo vertical. O nosso valor máximo vai estar dentro da região compreendida por todas as cores, ou seja, está naquele trapézio bem no meio da figura, que mistura as cores vermelha, azul e verde, sacou?
E agora, pra encontrar o valor máximo, a gente quer um ponto nesse espaço que esteja num vértice. Repara na fórmula da velocidade:
A contribuição de uma pressão alta é o que vai dar o máximo! Por isso, o nosso ponto que vai fornecer a máxima velocidade é o do vértice que está na ordenada de ! Nesse ponto, atmosferas. Fechou?