Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 14.4 - Ex. 9

Ache os pontos de máximo e os pontos de mínimo da função f x , y = 7 x + 5 y + 2 definida na região determinada pelas desigualdades:

2 x + y + 9 ≥ 0 - x + 2 y + 6 ≥ 0 x ≥ 0 x + y - 4 ≤ 0

Passo 1

Vamos começar dando uma ajeitada nas equações:

y ≥ - 2 x - 9 y ≥ x 2 - 3 y ≤ - x + 4 x ≥ 0

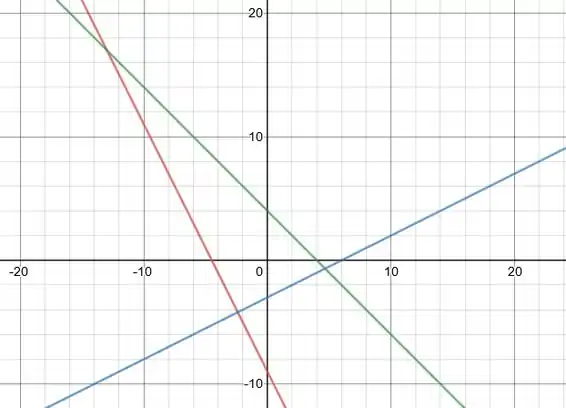
A região que a gente quer está acima da reta vermelha, acima da reta azul, e abaixo da reta verde. Além disso, como x ≥ 0 , só vale o que está à direita do eixo y .

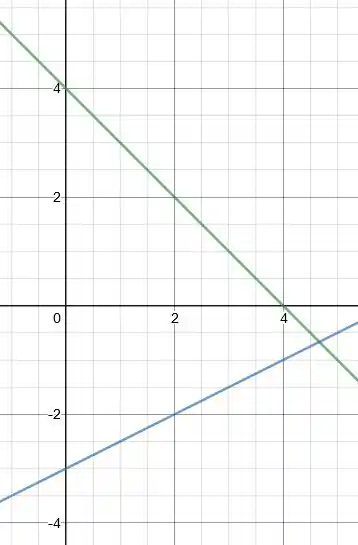
Passo 2

Beleza, a gente quer achar o máximo da função f x , y = 7 x + 5 y + 2 nessa região limitada. Isso é equivalente a achar o máximo de 7 x + 5 y e somar 2 , né? Então vamos fazer desse jeito. O vetor perpendicular a 7 x + 5 y é ( - 5 ,   7 ) . Vamos desenhar uma reta nessa direção passando pela origem.

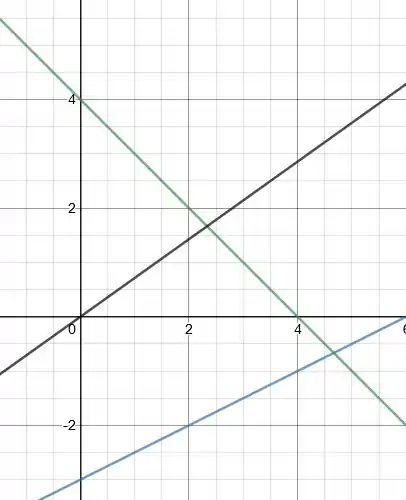
O encontro dessa reta preta com a verde vai ser o ponto de máximo!

- 5 x + 7 y = 0 y = - x + 4

Substituindo a segunda na primeira:

- 5 x + 7 - x + 4 = 0

- 5 x - 7 x + 28 = 0

Assim,

x = 7 3

E substituindo,

y = - 7 3 + 4

y = 5 3

Portanto, o máximo da função é:

f x , y = 7 x + 5 y + 2

f 7 3 , 5 3 = 7 7 3 + 5 5 3 + 2

f 7 3 , 5 3 = 83 2

Passo 3

Agora pra acharmos o mínimo, faz assim: a gente quer o menor valor possível de 7 x + 5 y + 2 . Aí se liga: o menor valor de x já é o 0 , não tem como fugir. Então vamos botar o menor valor possível de y nessa região, que do gráfico é y = - 3 . Assim:

f 0 ,   - 3 = 5 - 3 + 2

f 0 ,   - 3 = - 13

Resposta

Máximo: 83 2

Mínimo: - 13

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolva o sistema de equações, escrevendo as matrizes ampliadas, associadas aos novos sistemas. 2 x - y + 3 z = 11 4 x - 3 y + 2 z = 0 x + y + z = 6 3 x + y + z = 4
Numa indústria química há uma caldeira cuja margem de segurança é tal que a pressão P é medida em atmosferas, e a temperatura T , medida em graus Celsius, devem ser reguladas de maneira que 10 P + T ≤
Seja A = 2 0,1 1 3 4 0 0 1 8 .Calcule A .Ao resolvermos o sistema A ⋅ x y z = 3 0 1 , podemos garantir que o processo iterativo dado por X n = M X + N onde M = I - A e N = 3 0 1 converge para uma solu
Se duas regiões poliedrais convexas são definidas por dois conjuntos de desigualdades lineares, a interseção destas regiões é definida por qual conjunto de desigualdades?
Para o sistema linear dado, encontre todos os valores de a para os quais o sistema não tem solução, tem solução única e tem infinitas soluções: x + 2 y + z = 3 x + y - z = 2 x + y + a 2 - 5 z = a