Exercícios de Análise de Solução de um Sistema Linear - Lista de Exercícios Resolvida

Associe a cada sistema abaixo (uma letra) o problema correspondente (um número):

Para quais valores de o sistema linear abaixo é possível e determinado?

Seja um sistema de equações lineares possível , tal que .

Seja o conjunto das soluções gerais de e do sistema homogêneo.

Prove que se e , então .

Determine os valores de para que o sistema possua:

1. Uma única variável livre
2. Duas variáveis livres

Para cada um dos itens abaixo, dê um exemplo de um sistema com as características pedidas ou explique por que tal exemplo não pode existir.

1. ( equações) ( variáveis), infinitas soluções
2. ( equações) ( variáveis), solução única
3. ( equações) ( variáveis), nenhuma solução
4. ( equações) ( variáveis), infinitas soluções

Determine e para que o sistema abaixo seja possível indeterminado.

Classifique o sistema a seguir.

Seja . Mostre que se (representados como vetores coluna) são soluções do sistema linear homogêneo , então tambem é solução do sistema linear homogêneo .

Encontre condições que a constante deve satisfazer para que o sistema seja consistente.

(b)

Encontre condições que a constante deve satisfazer para que o sistema seja consistente.

(d)

Para que valor(es) de o sistema de equações

tem soluções não-triviais?

Use a parte (a) para mostrar que o sistema

tem exatamente uma solução quando .

1) Quais dos seguintes sistemas são lineares em e ?

a)

1) Quais dos seguintes sistemas são lineares em e ?

d)

1) Quais dos seguintes sistemas são lineares em e ?

c)

2) Encontre o conjunto solução de cada uma das seguintes equações lineares.

b)

Encontre condições que a constante deve satisfazer para que o sistema seja consistente.

(c)

34) Seja um sistema de equações lineares consistente e seja uma solução fixada. Mostre que qualquer solução do sistema pode ser escrita na forma , onde é a solução de . Mostre também que qualquer matriz dessa forma é uma solução.

Considere o sistema de equações e incógnitas.

Qual das seguintes situações não pode acontecer?

, nenhuma solução

, mais de uma solução

, nenhuma solução

, solução única

Para quais valores da constante o sistema:

Não tem solução? Exatamente uma solução? Infinitas soluções? Explique o seu raciocínio.

12. Assinale a alternativa FALSA:

(a) Se e , então não é combinação linear das colunas de

(b) Se e , então não tem solução

(c) Se , então é combinação linear das colunas de

(d) Se e , então não tem solução

(e) Não sei

Determine o valor de para que o sistema linear , e tenha uma única solução.

Com relação ao sistema linear com , considere as afirmações abaixo:

(I) Se e são soluções de S, então é solução de

(II) Se S não admite solução, então não admite solução.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Classifique as afirmativas abaixo:

– Existem dois números positivos tais que a razão entre a sua diferença e a sua soma é igual a razão entre eles.

– Existem dois números positivos tais que a razão entre a sua soma e a sua diferença é igual a razão entre eles.

a) Ambas são verdadeiras

b) é falsa e é verdadeira

c) Ambas são falsas

d) é verdadeira e é falsa

e) Não sei

Considere o seguinte sistema de equações lineares:

a)Determine os valores de para os quais o sistema tem infinitas soluções, e determine o conjunto solução.

b)Para que valores de o sistema não tem solução?

c)O sistema acima com tem matriz ampliada linha-equivalente à matriz ampliada do seguinte sistema?

Considere o sistema abaixo, onde os coeficientes, são números não nulos:

1. pode ter solução única
2. sempre tem solução

1. I é verdadeira e II é falsa
2. Ambas são falsas
3. Ambas são verdadeiras
4. I é falsa e II é verdadeira

O valor de para que o sistema

Nas incógnitas tenham infinitas soluções é:

Seja um inteiro positivo, e sejam e . Denote a matriz transposta de por . Utilizando a notação matricial para sistemas lineares, está correto afirmar que

Escolha uma:

a) Se tem infinitas soluções, então tem infinitas soluções

b) Se tem apenas a solução trivial, então tem apenas a solução trivial

c) Se tem uma única solução, então tem infinitas soluções

d) Se não tem solução, então tem apenas a solução trivial

e) Se tem infinitas soluções, então tem infinitas soluções

Considere os sistemas : e . Verifique as afirmações abaixo:

I - Se o sistema tem solução, então o sistema tem solução

II - Se o sistema tem solução única, então o sistema tem solução única

(a) Ambas são falsas

(b) I é falsa e II é verdadeira

(c) I é verdadeira e II é falsa

(d) Ambas são verdadeiras

Qual destas equações, se acrescentada ao sistema linear abaixo como uma terceira equação, resultará em um sistema de solução única?

(a)

(b)

(c)

(d)

Considere o sistema linear representado pela seguinte matriz aumentada:

Assinale o valor de de forma que o sistema tenha solução:

(a) 3

(b) 1

(c) 0

(d) 2

Sejam , , e números quaisquer. O sistema:

nunca tem solução

sempre tem várias soluções

só tem solução se

só tem solução se

Considere a matriz.

Em b) e c) considere que esta é a matriz ampliada de um sistema de equações lineares.

b) Determine para que valores de k este sistema não teria solução.

c) Para o(s) caso(s) em que o sistema é possível, determine o conjunto solução.

Os vetores , e do são as colunas da matriz aumentada de um sistema linear:

Considere as seguintes situações distintas:

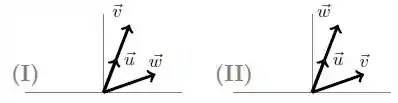
(a) O sistema (I) tem solução única.

(b) O sistema (I) tem infinitas soluções.

(c) O sistema (II) tem solução única.

(d) O sistema (II) tem infinitas soluções.

Considere o sistema:

Faça o que se pede abaixo:

i. Determine os valores de a e b para que o sistema tenha uma única solução e calcule sua solução.

ii. Determine os valores de a e b para que o sistema tenha infinitas soluções e calcule suas soluções.

iii. Determine os valores de a e b para que o sistema não tenha soluções.

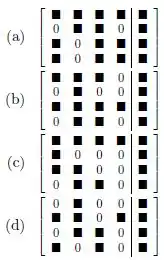
Considere o sistema S representado pela matriz aumentada

onde é um conjunto linearmente independente. Assinale a matriz aumentada que representa um sistema equivalente a S.

(a)

(b)

(c)

(d)

Cada representa um número diferente de 0. (Diferentes ’s podem assumir valores distintos!). O sistema que pode não ter solução é:

A matriz aumentada representa um sistema linear. A alternativa INCORRETA é:

a) Se o sistema admite solução, então .

b) Se , o sistema não possui solução.

c) Se , o sistema possui solução única.

d) Quaisquer que sejam e , o sistema não possui solução única.

e) Não sei.

Quais são todos os possíveis valores de e para que o sistema linear a seguir tenha solução única?

a)

b)

c)

d)

e) Não sei.

Considere o sistema linear

a) Justifique porque, independente dos valores que adotarmos para , e , não pode ser solução do sistema acima.

Classifique em verdadeira ou falsa as afirmativas abaixo:

I - Um sistema linear com mais equações do que incógnitas nunca tem infinitas soluções

II - Um sistema linear com mais incógnitas do que equações sempre tem infinitas soluções

(a) Ambas são falsas

(b) I é verdadeira e II é falsa

(c) Ambas são verdadeiras

(d) I é falsa e II é verdadeira

Sejam e números não nulos e e números quaisquer. O sistema:

nunca tem solução

sempre tem várias soluções

só tem solução se

só tem solução se

Quais das expressões abaixo representa a solução geral da equação .

Se , é correto afirmar que o sistema linear

1. Possível e indeterminado se, e somente se, ;
2. Possível e determinado se, e somente se, e ;
3. Impossível se, e somente se, ;
4. Possível e determinado se, e somente se, ;
5. Impossível se, e somente se, ;

2) Encontre o conjunto solução de cada uma das seguintes equações lineares.

a)

2) Encontre o conjunto solução de cada uma das seguintes equações lineares.

c)

4) Mostre que as equações e têm o mesmo conjunto-solução, então as equações são idênticas.

10) O sistema seguinte não tem solução para quais valores de ? Exatamente uma solução? Infinitas soluções?

Considere o sistema de equações lineares

Onde é um número real

c) Determine as soluções do sistema no caso em que e as escreva na forma vetorial paramétrica

Considere os seguintes sistemas lineares:

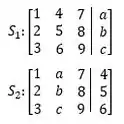
(I) Existem valores de a, b e c tais que o sistema não tem solução.

(II) Existem valores de a, b e c tais que o sistema não tem solução.

(a) I é verdadeira e II é falsa

(b) I é falsa e II é verdadeira

(c) Ambas são verdadeiras

(d) Ambas são falsas

Sejam a e b e considere o sistema linear:

Nas incógnitas reais e . Temos que esse sistema possui uma única solução se, e somente se:

1. b = 2 a
2. a = 1

Seja e considere o sistema linear

Nas incógnitas reais . Temos que esse sistema possuirá uma única solução se, e somente se:

Sejam e considere as afirmações sobre o sistema linear

nas incógnitas x,y,z:

Considere um sistema linear com m equações em n incógnitas. Pode-se afirmar que:

(a) Se , a solução, se existir, será única.

(b) Se , a solução, se existir, não será única.

(c) Se , a solução, se existir, será única.

(d) Se , a solução, se existir, não será única.

Seja um sistema com 5 equações e 3 variáveis e um sistema com 3 equações e 5 variáveis, ambos homogêneos. Sejam e seus respectivos conjuntos-solução. Considere as afirmativas:

Pode-se afirmar que

Pode-se afirmar que

a) é verdadeira e é falsa

b) é verdadeira e é verdadeira

c) é falsa e é verdadeira

d) é falsa e é falsa

e) Não sei.

Sejam . Então, o sistema linear

Nas variáveis é impossível se, e somente se,

Escolha uma:

a) e

b) e

c) e

d) e

e) e

Seja e . Considere as seguintes afirmações sobre o sistema linear e sobre o sistema linear homogêneo associado :

1. Se tem infinitas soluções, então tem infinitas soluções

2. Se tem uma única solução, então só tem a solução trivial

3. Quando , é possível que só tenha a solução trivial e não tenha solução

a) Apenas 1 é verdadeira

b) Apenas 2 e 3 são verdadeiras

c) Apenas 3 é verdadeira

d) 1, 2 e 3 são falsas

e) 1, 2 e 3 são falsas

f) Apenas 1 e 2 são verdadeiras

g) Apenas 1 e 3 são verdadeiras

h) Apenas 2 é verdadeira

Considere o sistema de equações lineares abaixo. Encontre a(s) condição(ões) sobre a, b e c para que o sistema seja possível. E, neste caso, diga qual o grau de liberdade do sistema.

(I) Um sistema linear com mais equações do que incógnitas pode ter solução única.

(II) Um sistema linear com menos equações do que incógnitas pode ter solução única.

(a) I é verdadeira e II é falsa

(b) I é falsa e II é verdadeira

(c) Ambas são verdadeiras

(d) Ambas são falsas

São dadas as inversas das matrizes .

Calcule a solução do sistema linear

O valor da primeira entrada de é:

1. 2
2. -1
3. 1
4. 0

As matrizes aumentadas abaixo representam, respectivamente, os sistemas lineares e :

Considere as afirmativas:

pode ter infinitas soluções mesmo quando tem solução única.

pode ter infinitas soluções mesmo quando tem solução única

a) é verdadeira e é verdadeira

b) é falsa e é falsa

c) é verdadeira e é falsa

d) é falsa e é verdadeira

e) Não sei.

Considere as afirmativas:

Um sistema linear com menos equações do que incógnitas sempre tem solução.

Um sistema linear com mais equações do que incógnitas nunca tem solução.

a) é falsa e é verdadeira

b) é falsa e é falsa

c) é verdadeira e é falsa

d) é verdadeira e é verdadeira

e) Não sei.

Seja e considere o sistema linear homogêneo

Nas incógnitas reais e . Temos que esse sistema possui apenas a solução trivial se, e somente se

a)

b)

c)

d)

e)

Considere o sistema de equações lineares

Onde é um número real

b) Com base na matriz obtida no item (a), determine para quais valores de o sistema não admite solução, para quais admite uma única solução, e para quais valores admite infinitas soluções.

Fixe e considere o sistema linear

É correta afirmar que

Diga se as afirmativas abaixo são verdadeiras ou falsas.

1. Um sistema linear com mais equações que incógnitas sempre possui solução.
2. Um sistema linear com menos equações que incógnitas sempre possui solução.

I é falsa e II é verdadeira

Ambas são falsas

Ambas são verdadeiras

I é verdadeira e II é falsa

Sejam . Sobre o sistema linear

Nas incógnitas é corretor afirmar que

, então o sistema tem exatamente uma variável livre

o sistema é compatível, para quaisquer

não existe valor de para os quais o sistema seja compatível indeterminado

se o sistema for compatível indeterminado, então

o sistema é compatível determinado se, e somente se,

Considere o problema de se encontrar dois números cuja soma seja igual a a, cuja diferença seja igual a b e tais que o triplo do primeiro mais o quíntuplo do segundo seja igual a c.

(a) Quando este problema tem solução, ela é única.

(b) Este problema nunca tem solução.

(c) Este problema sempre tem solução.

(d) Quando este problema tem solução, ela não é única.

1) Quais dos seguintes sistemas são lineares em e ?