Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 14.4 - Ex. 3
Desenhe a região definida em pelas desigualdades anteriores.
Passo 1
Galera, o nosso sistema era:
Show, ele quer que a gente desenhe essa região no . Mas ué, tá vendo que não tem envolvido? Então essa parada vai estar toda no plano ! Não vai ter nada saindo do plano, sacou?
Passo 2
Isso quer dizer que uma visão do já é mais do que suficiente pra gente conseguir visualizar a parada no , só vai ficar faltando a setinha saindo da origem pra fazer o eixo , hahahah
Então a região vai ficar assim no plano , com adição do eixo :
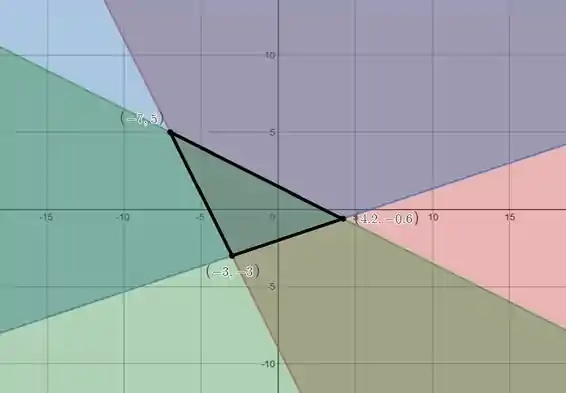
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A união de dois conjuntos convexos é convexa?
Quais são os vértices da região poliedral convexa em R 2 , definida por x ≥ 0 2 x + 3 y ≤ 2 3 x + 2 y ≤ 2 x + y ≤ 1 Desenha esta região.
Ache os pontos de máximo e os pontos de mínimo da função f x , y = 7 x + 5 y + 2 definida na região determinada pelas desigualdades: 2 x + y + 9 ≥ 0 - x + 2 y + 6 ≥ 0 x ≥ 0 x + y - 4 ≤ 0
Sejam A = ( 1 ,2 ,3 ) e B = ( 0 ,1 ,- 1 ) dois pontos de R 3 . O ponto ( 0 ,0 ,0 ) está sobre o segmento A B ?