Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 9.Exercício - Ex. 6
Os lados do triângulo equilátero têm medida 2. Calcule .
Passo 1
O primeiro passo é identificar o ângulo entre os vetores:
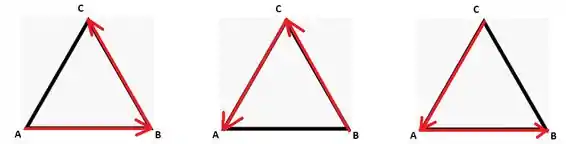
Em todos os casos, o ângulo entre os vetores é . Além disso, temos que .
Passo 2
Assim, usando a fórmula do produto escalar:
Portanto,
Logo,
Resposta
Exercícios de Livros Relacionados
Observando a figura ao lado, diga se os vetores são l.i. ou l.d. e justifique cada resposta. b → , c → e y → ; a → , x → e y → ; a → , b → , x → e y → ; a → , w → , com w → =x →-a→ +b → .
Tem-se: a →= ( 1 , - 1,2 ) , b →=( 1,1 , 0 ) e c →=( 1,1 , - 1 ) e d →=( 1,0 , - 1 ) . O vetor x → é coplanar com a → e b → e x→ + d → / /c → . Determine as coordenadas de x → .Escreva x → como combin
No ΔA B C temos A B →= ( 2 , - 1 , - 2 ) e A C →= ( 3,5 , - 1 ) . Pedem-se:a projeção ortogonal de A C → na direção de A B → ;um vetor não nulo H C → que dê a direção da altura relativa ao vértice C;o
Os vetores a → e b → formam um ângulo de 60 ° , | a | →= 1 e | b | →= 2 . Sabe-se que u →= a → +3 b → e v →= 2 a → -b → . Pedem-se: | u | → , | v | → e o ângulo formado por u → e v → . Desenhe os veto
Demonstre que se V e W são vetores quaisquer, então:b) V + W ≤ V + W