Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 3.Exercícios Propostos - Ex. 18
No temos e . Pedem-se:
- a projeção ortogonal de na direção de ;
- um vetor não nulo que dê a direção da altura relativa ao vértice C;
- o comprimento da altura relativa ao vértice C;
- as coordenadas do vetor , sendo o ponto simétrico de em relação à reta suporte do lado AB.
Passo 1
Fala, galerinha! Estão preparados?
- Lembraremos que a projeção de um vetor na direção de é dada por:
- Desenhamos o , juntamente com a altura relativa ao vértice C, que deve ser ortogonal a aresta oposta. Então, o produto interno entre e deve ser nulo. Vemos que deve ser uma combinação linear entre e , ou seja,
- O ângulo entre os vetores e tem um cosseno dado por
- Antes de mais nada, vamos usar o resultado do item c) para descobrir , uma vez que é proporcional a . Então, tirando o módulo dos dois vetores, devemos ter
.
Passo 2
Como , então
Usando a condição de que e devem ser ortogonais, obtemos
Substituindo esse resultado em , obtemos
Como a questão pede um vetor não nulo que dê a direção da altura relativa ao vértice C, temos liberdade para escolher . Então, vamos escolher .
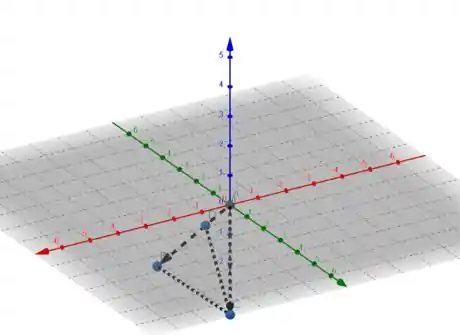
Passo 3
Por outro lado, esse cosseno também pode ser dado por
Comparando as duas expressões, encontramos que
Passo 4
Logo, devemos ter . O ponto que é simétrico a em relação à reta suporte do lado AB fica da seguinte forma
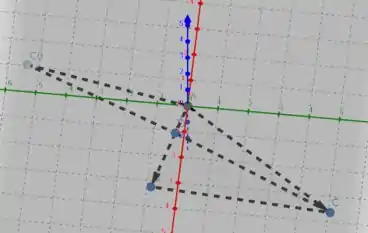
Então, vemos que o ponto está do lado oposto ao ponto C em relação a AB e D é o ponto onde a reta que sai de C a cruza o eixo AB. Logo, o vetor será dado pelo vetor central e pelo vetor . Pela geometria dos vetores, temos que
.
Resposta
- ;
- ;
- ;
- .