Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 7.Problemas - Ex. 8

Os lados de um triângulo estão sobre as retas y   =   2 x + 1 , y   =   3 x - 2 e y   =   1 - x . Ache os vértices desse triângulo.

Passo 1

Faaaala, galera! Essa questão é bem tranquila! Vamos lá concluir mais uma?

O triângulo em questão está sobre as retas informadas. Observe a imagem que representa as retas. Para obter os vértices do triângulo, basta encontrarmos as interseções A ,   B e C . A interseção é o ponto de encontro entre elas e é essa interseção que delimita o triângulo. Beleza?

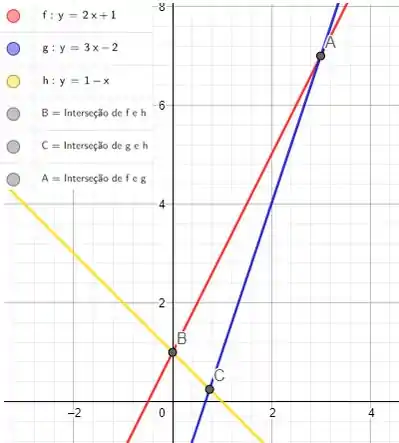
Agora vamos obter os pontos.

Interseção entre g e   f :

y = 2 x + 1   ( I )

y = 3 x - 2

Igualando as retas:

2 x + 1 = 3 x - 2

2 x - 3 x = - 2 - 1

- x = - 3

x = 3

Substituindo o valor de x em ( I ) , temos:

y = 2 3 + 1

y = 7

Interseção entre f e h :

y = 2 x + 1

y = 1 - x

Igualando:

2 x + 1 = 1 - x

2 x + x = 1 - 1

3 x = 0

x = 0

Substituindo em ( I ) :

y = 2 ( 0 ) + 1

y = 1

Interseção entre g e   h :

y = 3 x - 2

y = 1 - x         ( I I )

Igualando:

3 x - 2 = 1 - x

3 x + x = 1 + 2

4 x = 3

x = 3 / 4

Substituindo em ( I I ) :

y = 1 - x

y = 1 - 3 / 4

y = 4 / 4 - 3 / 4

y = 1 / 4

Prontinho!

Resposta

A ( 3,7 )  

B ( 0,1 )

C 3 4 , 1 4

Exercícios de Livros Relacionados

A reta que passa pelos pontos ( 4 , 1 , - 1 ) e ( 2 , 5 , 3 ) é perpendicular à reta que passa pelos pontos ( - 3,2 , 0 ) e 5,1 , 4 ?
Determine as equações simétricas da reta que passa pelo ponto 1 , - 5,6 e é paralela ao vetor ( - 1,2 , - 3 ) .Determine os pontos nos quais a reta da parte (a) intercepta os planos coordenados.
Ache a equação vetorial para o segmento de reta de ( 2 , - 1,4 ) a ( 4,6 , 1 ) .
A reta que passa pelos pontos ( - 4 , - 6,1 ) e ( - 2,0 , - 3 ) é paralela à reta que passa pelos pontos ( 10,18,4 ) e 5,3 , 14 ?
Ache as equações paramétricas para o segmento de reta de ( 10,3 , 1 ) a ( 5 , 6 , - 3 ) .