Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 3.Problemas Propostos - Ex. 50
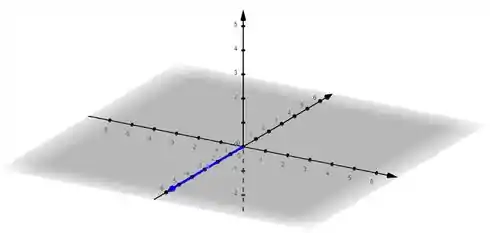
Mostrar num gráfico um representante de cada um dos seguintes vetores:
Passo 1
Nesse problema, o nosso desafio é mostrar em um gráfico um representante de cada um dos seguintes vetores:
Passo 2
a)
Podemos determinar este produto vetorial como:
Passo 3
Eis a solução no software Geogebra.
Basta digitar .
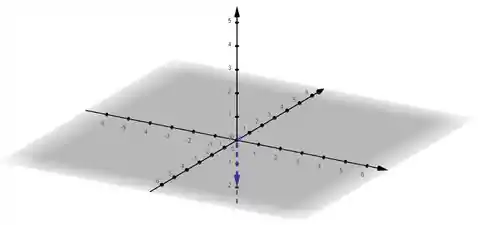
Passo 4
b)
Para este item, temos
Basta usarmos a mesma ideia que utilizamos no item a). Assim, obtemos:
E eis o nosso gráfico:
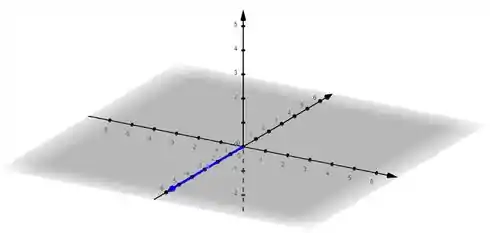
Resposta
a)
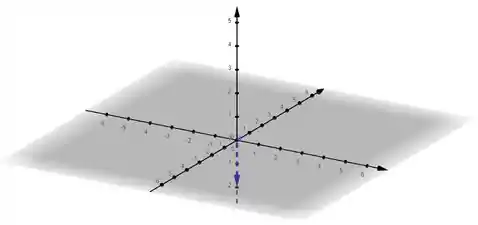
b)
Exercícios de Livros Relacionados
Calcule a área do paralelogramo A B C D , sendo A B → = ( 1 ,1 ,- 1 ) e A D → = ( 2 ,1 ,4 ) .
Calcule a área do triângulo A B C , sendo A B → = ( - 1 ,1 ,0 ) e A C → = ( 0 ,1 ,3 ) .
O triângulo A B C tem área 4 . Sabendo que B = A + u → e C = A + v → , calcule u → ∧ v → .
A medida angular entre u → e v → é 30 ° , e suas normas, 2 e 3 . Calcule u → ∧ v → .
Sabendo que u → = 1 e v → = 7 e a n gu → ,v → = π / 6 , calcule u → ∧ v → e 4 u → ∧ 9 v → .