Mostre que a área do triângulo com vértices , para é igual à , em que
(Sugestão: Marque os pontos e . O volume do paralelepípedo determinado por é dado por Mas, a altura deste paralelepípedo é igual à 1. Assim, o seu volume é igual à área da base que é o paralelogramo determinado por . Observe que são paralelos ao plano .)
Passo 1
Opa! Tudo certinho contigo?
Vamos começar dando uma olhada neste paralelepípedo, saca só!
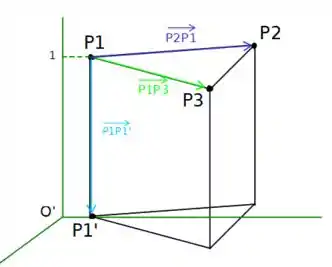
Okay! Agora analisando a sugestão do enunciado, vamos tomar que (Já que esta é a altura de nosso paralelepípedo!). Mas isso nos ajuda em que?
Passo 2
Beleza, temos que o volume do paralelepípedo é dado como o produto entre a base e a altura, da seguinte forma:
Uma vez que . Mas vamos lembrar de mais uma coisinha!
Passo 3
O volume de um paralelepípedo cuja base é um paralelogramo, pode ser calculado através do seguinte produto misto:
Os vetores são os seguintes:
Também temos que:
E
O produto misto toma então a forma;
Como estamos interessados no módulo, não importa se usamos ou , beleza? Se a matriz dentro do determinante acima puder ser identificada como (ou seja equivalente à) a matriz , nosso problema está resolvido! Vamos tentar fazer isso!
Passo 4
O determinante acima é tal que:
O determinante de resulta em:
Olha só que legal! O determinante da matriz é o mesmo do que o que calculamos no produto misto a menos de um sinal global negativo. Sendo assim, quando tirarmos o módulo não fará a menor diferença! Ou seja, o determinante da matriz (em módulo) é equivalente ao volume do paralelogramo, e assim, como , é equivalente a área do paralelogramo. Mas como isso mostra o que o enunciado nos pede??
Passo 5
Vamos comparar a área de um paralelogramo gerado pelos pontos com a área de um triângulo que tem estes pontos como vértice! Olha o esquema a seguir:
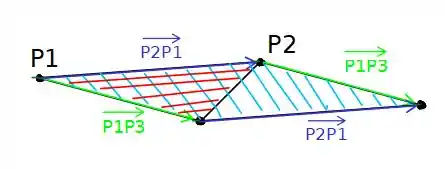
Os traços em azul indicam e os traços vermelhos . Portanto podemos garantir que:
A questão foi isso, te vejo na próxima! Tchauzinho!
Resposta
Ao longo dos passos!