Enunciado
Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 4.2 - Ex. 4
Observe que:
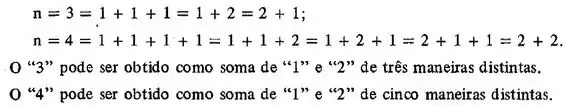
Faça o mesmo com .
Passo 1
Oi, tudo bem? Bora resolver mais um exercício?
Se não se lembra desse conteúdo, é hora de dar aquela revisão. Ok?
Passo 2
Vamos lá!
Realizando o processo do enunciado, temos:
Resposta
Assim, conclui-se a questão.
Exercícios de Livros Relacionados
Mesma questão, com x n + 4 = 5 x n + 3 - 5 x n + 2 - 5 x n + 1 + 6 x n .
Seja S o subconjunto das sequências ( x 0 ,x 1 , … ,x n , … ) tais que x n + 3 = 6 x n + 2 - 11 x n + 1 + 6 x n . Provar que S é subespaço vetorial dos reais infinito e encontrar uma base.
( x 0 , x 1 , … , x m , … ) tais que x n + 1 = a x n + b x n - 1 . Achar uma base de S nos casos:
( x 0 , x 1 , … , x m , … ) tais que x n + 1 = a x n + b x n - 1 . Achar uma base de S nos casos: