Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 29.Problemas - Ex. 2

Obtenha uma equação para o plano que contém o ponto P e é perpendicular ao segmento de reta A B nos seguintes casos:

a )   P   =   ( 0 ,   0 ,   0 ) ,   A   =   ( 1 ,   2 ,   3 ) ,   B   =   ( 2 ,   - 1 ,   2 ) ;  

b )   P   =   ( 1 ,   1 ,   - 1 ) ,   A   =   ( 3 ,   5 ,   2 ) ,   B   =   ( 7 ,   1 ,   12 ) ;  

c )   P   =   ( 3 ,   3 ,   3 ) ,   A   =   ( 2 ,   2 ,   2 ) ,   B   =   ( 4 ,   4 ,   4 ) ;  

d )   P   =   ( x 0 ,   y 0 ,   z 0 ) ,   A   =   ( x 1 ,   y 1 ,   z 1 ) ,   B   =   ( x 2 ,   y 2 ,   z 2 ) .

Passo 1

Saudações galerinha, tudo bem?

Vamos começar a resolver mais um exercício, bora lá então!

Inicialmente vamos encontrar a equação das retas AB, vou encontrá-la utilizando a condição de alinhamento entre pontos.

Lembra?

Relaxa basta resolver o determinante:

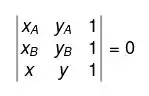
Vamos aplica-lá então!

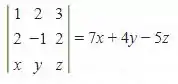
Para encontrar a equação do plano basta aplicar a condição:

P Q →   .   v → = 0  

Logo a equação do plano será:

1 ( x - 0 ) +   2 ( y - 0 ) +   3 ( z - 0 ) =   0

x +   2 y +   3 z =   0

Passo 2

Para P   =   1 ,   1 ,   - 1 ,   A   =   3 ,   5 ,   2 ,   B   =   7 ,   1 ,   12 , vamos repetir o item anterior

Aplicando a condição de alinhamento vamos obter:

Para encontrar a equação do plano basta aplicar a condição:

P Q →   .   v → = 0  

Logo a equação do plano será:

3 ( x - 1 ) +   5 ( y - 1 ) +   2 ( z + 1 ) =   0

3 x - 3 +   5 y - 5 +   2 z + 2 =   0

3 x +   5 y +   2 z =   6

Passo 3

Para P   =   ( 3 ,   3 ,   3 ) ,   A   =   ( 2 ,   2 ,   2 ) ,   B   =   ( 4 ,   4 ,   4 ) ;   , vamos repetir o item anterior

Aplicando a condição de alinhamento vamos obter:

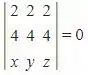
Para encontrar a equação do plano basta aplicar a condição:

P Q →   .   v → = 0  

Logo a equação do plano será:

3 ( x - 2 ) +   3 ( y - 2 ) +   3 ( z - 2 ) =   0

3 x - 6 +   3 y - 6 +   3 z - 6 =   0

3 x +   3 y +   3 z =   18

Passo 4

Quase acabando!

Para P   =   ( x 0 ,   y 0 ,   z 0 ) ,   A   =   ( x 1 ,   y 1 ,   z 1 ) ,   B   =   ( x 2 ,   y 2 ,   z 2 ) , vamos repetir o item anterior

Para esse exercício em especifico vou fazer a troca x 1 = a ,   y 1 = b ,   z 1 = c ; x 2 = f ,   y 2 = e ,   z 2 = d

Aplicando a condição de alinhamento vamos obter:

Para encontrar a equação do plano basta aplicar a condição:

P Q →   .   v → = 0  

Logo a equação do plano será:

x 0 ( x - a ) +   y 0 ( y - b ) +   z 0 ( z - c ) =   0

Prontinho!

Acabamos te vejo na próxima questão!

Resposta

a) x +   2 y +   3 z =   0

b)

3 x +   5 y +   2 z =   6

c)

3 x +   3 y +   3 z =   18

d)

x 0 ( x - a ) +   y 0 ( y - b ) +   z 0 ( z - c ) =   0

Exercícios de Livros Relacionados

Sendo x = 1 + h - 2 t y = 1 - t z = 4 + 2 h - 2 t Equações paramétricas de um plano π , obter uma equação geral.
Determinar uma equação geral do plano que passa pelos pontos A ( - 3 ,1 ,- 2 ) e B ( - 1 ,2,1 ) e é paralelo à reta r : x 2 = z - 3 ; y = 4
Nos problemas 7 - 11 , escrever uma equação geral e um sistema de equações paramétricas do plano determinado pelos pontos:9) A 2,0 , - 1 , B - 2,6 , 3 ,C ( 0,3 , 4 ) .
Nos problemas 7 - 11 , escrever uma equação geral e um sistema de equações paramétricas do plano determinado pelos pontos:10) A 2,1 , 0 , B - 4 , - 2 , - 1 ,C ( 0,0 , 1 ) .
Determinar uma equação geral do plano que contém os pontos A ( 1 ,- 2 ,2 ) e B ( - 3 ,1 ,- 2 ) e é perpendicular ao plano π : 2 x + y - z + 8 = 0 .