Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 14.Exercício - Ex. 23
Obtenha equações paramétricas dos planos coordenados.
Passo 1
Todos os planos coordenados passam pela origem , como podemos ver na figura:
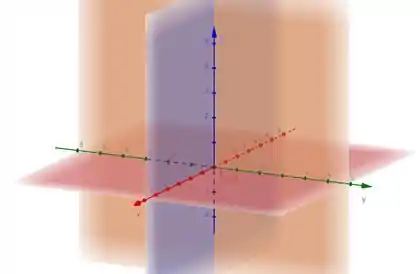
No plano roxo, que vamos chamar de , é sempre 0, pois pode perceber que ele não tem nenhuma coordenada no eixo .
Então os vetores diretores desse plano são e e suas equações paramétricas são:
Passo 2
No plano vermelho, que vamos chamar de , é sempre 0.
Então os vetores diretores são e e suas equações paramétricas são:
Passo 3
No plano laranja, , é sempre 0, então os vetores diretores são e :
Resposta
Exercícios de Livros Relacionados
Identifique geometricamente os seguintes conjuntos E={ ( x ,y ,z )∈R 3;| x |≤1 ,| y |≤1e| z |≤1 }
Um plano vertical Π corta os eixos OX e OY nos pontos A = (3, 0, 0) e B = (0, −1, 0). Determine os coeficientes a, b, c, d de modo que um ponto P = (x, y, z) pertença a Π se, e somente se, ax + by + c
Identifique geometricamente os seguintes conjuntos J ={ ( x ,y ,z )∈R 3;x-z 2+y-z 2 ≤1 }
Escreva a equação de um plano vertical que contenha as soluções de ambos os sistemas a seguir. Quantos planos têm essa propriedade? x - 2 y + 3 z = 5 x - 7 y + 14 z = 13 2 x + y - 5 z = 2 4 x - 3 y +
Identifique geometricamente os seguintes conjuntos: F={ ( x ,y ,z )∈R 3;x y=1 ,x0 ,y0 }