Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 17.Exercício - Ex. 35
Determine os vértices , e de um quadrado , sabendo que , um lado está contido no plano , outro, no plano , e o plano do quadrado é perpendicular à reta intersecção de e .
Passo 1
Bom, o primeiro passo é verificar se o ponto pertence a um dos lados contidos nos planos e . Vemos que esse ponto não satisfaz nenhuma das equações. Com isso podemos fazer um esboço:
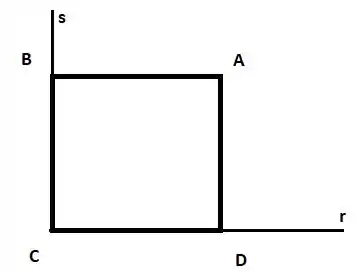
A reta está contida no plano e a reta no plano . Portanto, os pontos e são do tipo
e os pontos e são do tipo
O ponto deve pertencer deve satisfazer as duas relações simultaneamente:
Substituindo a primeira equação na segunda:
Substituindo de volta na primeira equação:
Portanto, o ponto é do tipo
Para não ficar carregando a letra , o que pode dar muita confusão mais para frente, vamos usar a letra :
O que fizemos aqui na verdade foi achar a intersecção dos planos e , que é uma reta. O ponto está contido nessa reta! Note que podemos abrir a equação dessa reta:
Portanto, o vetor diretor dessa reta é . O enunciado também disse que esse reta é perpendicular ao plano do quadrado, que chamaremos de nessa resolução. Sendo assim, o vetor normal ao plano do quadrado é
Passo 2
Desta forma, o vetor deve ser perpendicular ao vetor . Vamos achar primeiro:
Portanto,
Assim,
Logo,
Já achamos o ponto ! Vamos calcular a norma de para determinar a diagonal do quadrado:
Como , obtemos o lado do quadrado:
Passo 3
Vamos procurar agora o ponto , que deve ser da forma
Assim,
Esse vetor está no plano do quadrado, de modo que deve ser perpendicular a :
Assim,
Portanto,
Logo,
Sabemos que . Desta forma,
Abrindo a expressão:
Portanto,
Portanto, o ponto é
Passo 4
Por fim, vamos atrás do ponto :
Assim,
Logo,
Portanto,
Assim, como :
Logo,
Ou ainda,
Assim,