Obtenha um plano , paralelo a , que satisfaz a condição especificada em cada caso (o sistema de coordenadas é ortogonal).

a) intercepta o eixo em um ponto que dista do ponto .

b) intercepta os eixos coordenados nos vértices de um triângulo de área .

a) O eixo é uma reta que passa pela origem e tem vetor diretor , ou seja:

Queremos saber qual o ponto dessa reta que o nosso plano passa, o que sabemos sobre esse ponto?

Primeiro, esse ponto pode ser escrito de forma genérica pela equação da reta:

E segundo, esse ponto dista do ponto , então, pela fórmula de distância entre pontos:

Elevando os dois lados ao quadrado:

Substituindo no ponto , temos duas alternativas de ponto:

Então, vamos ter também duas opções de plano, substituindo na equação do plano :

E agora o ponto :

Logo, as opções de plano aqui são

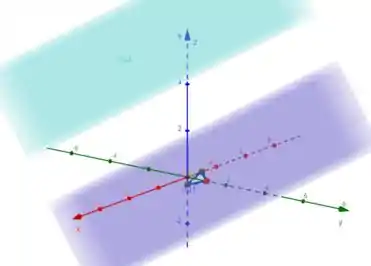
Aí embaixo temos em roxo os dois planos que encontramos, em azul o plano do enunciado e em rosa os pontos de intersecção dos planos com o eixo :)

b) Os vértices do triângulo que temos são dados por não é? Porque eles estão nos eixos coordenados.

Além disso, esses 3 vértices também passam pelo plano , então substituindo cada um desses pontos no plano, temos as relações:

Beleza, encontramos uma relação entre os vértices e o valor de que queremos encontrar hehe

Então os nossos vértices do triângulo são:

Sabemos que a área desse triângulo é dada por né?

Então:

Logo:

Calculando o módulo do vetor:

O enunciado nos diz que a área do triângulo é

Como encontramos dois valores para , temos duas alternativas de planos:

Aí embaixo, em azul temos o plano do enunciado, em roxo temos o plano e o triângulo que ele forma com os eixos coordenados :)