Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 2.6 - Ex. 28
Uma placa quadrada de material homogêneo é mantida com os bordos e à temperatura de , o bordo a e a , com o uso de isolantes térmicos em (vide figura).
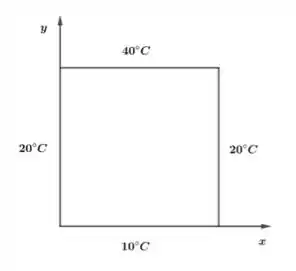
Após ser atingido o equilíbrio térmico, qual é a temperatura aproximada em cada ponto da placa?
Passo 1
Essa questão parece não ter nada a ver com álgebra linear à primeira vista, mas a grande sacada é modelar a placa fornecida como se fosse uma malha, veja na figura abaixo:
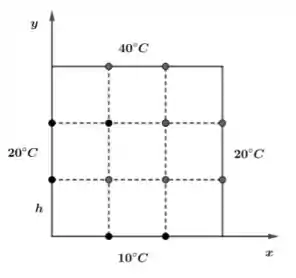
Obviamente, quanto mais fina for a malha, isto é, quanto menor for o , melhor será nossa aproximação do problema, concorda? Veja que quando fazemos tender a zero, obtemos a placa, onde a temperatura varia de maneira contínua e não discreta com a posição.
Passo 2
Vamos agora lembrar de nossos conhecimentos da física. Sabemos que esse problema é modelado pela seguinte equação:
Mas no estado estacionário, temos que , e aí resulta:
Tá, mas e daí?
E daí que precisamos usar isso para relacionar as temperaturas de um ponto com as temperaturas dos vizinhos. Mas como fazemos isso?
Passo 3
Não é nosso objetivo entender como se obtém isso, mas é possível mostrar que:
Substituindo as equações e na equação , obtemos:
Que, arrumando, fica:
Interpretando essa equação, o que ela significa?
Significa que a temperatura em um dado ponto da malha é a média aritmética das temperaturas dos seus vizinhos.
Passo 4
Conforme modelamos, nossa malha tem 16 pontos, o que já é bastante, uma vez que o objetivo dessa questão é apenas mostrar como a álgebra linear pode ser útil em problemas reais de engenharia com a ajuda da computação.
Observe na nossa figura que:
Usando a relação para determinar a temperatura dos pontos do interior da placa, temos:
Reorganizando esse sistema de equações, temos que:
Por fim, basta apenas resolver o sistema linear acima para encontrar as temperaturas em cada ponto da malha.